Volume d'une pyramide

Bonjour j'ai besoin de votre aide dans mon DM de maths que je comprends pas merci

Une pyramide a pour base un carré de côté c (en cm) et a pour hauteur h (en cm). On note a l'aire de la base en cm² et V le volume en $cm^3$ de la pyramide

a. Pour c=3 cm et h =4,5 cm, calculer une valeur approchée au dixième près du volume V de cette pyramide

b. Créez algorithme qui permet de saisir les valeurs de c et h qui calcule V, et qui affiche V

Merci

Bonjour,

Rappel pour démarrer ,

$base×hauteurV=\frac{1}{3} \times aire \ de \ la \ base \times hauteur$

$V=13×a×hV=\frac{1}{3}\times a \times h$

Ici, vu que la base est un carré de côté c , $a=c^2$

$\fbox{V=\frac{1}{3}\times c^2\times h}$

Propose tes réponses si tu as besoin d'une vérification.

@mtschoon

a. Alors 1/3 x 3^x 4,5 =13,5

Pour

b. Variables : c,h,s et v

Entréeh : saisir c,h

Traitement: S,prend la valeur de c
V prend la valeur de h
Sortie: afficher V

Oui pour la question a.
Remarque : c'est bizarre que l'énoncé te précise qu'il faut donner une valeur approchée au dixième près du volume V alors que 13.5 est la valeur exacte.

Pour la question b, revois la partie "traitement" car on ne comprend guère comment est calculé V

@mtschoon

Traitement. S prend la valeur 1/3
V prend la valeur de 1/3 x c^ x 4,5

Je ne vois pas l'interêt de cette variable S
La hauteur h ne vaut pas forcément 4.5 . c'est une donnée que doit saisir l'utilisateur
V=1/3 x c² x h

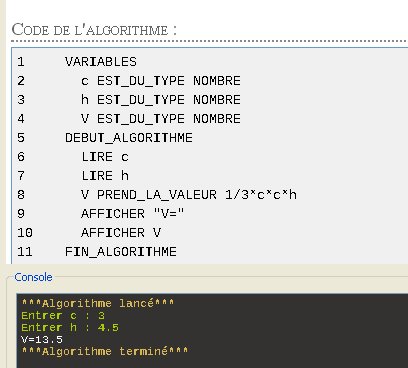
Si ça t'intéresse je te joins un algorithme fait avec Algobox (logiciel gratuit que tu peux télécharger sur ton PC) qui permet d'écrire des algorithmes et de les tester pour pouvoir s'assurer qu'ils sont exacts.