Exercice Maths Sangaku

Bonjour, pourriez vous m'aider je ne comprends pas du tout cette exercice

Une boule et un cochonnet sont placés dans une boîte carrée de côté 27 cm. Le rayon de la boule est 4 fois celui du cochonnet. Quels sont leurs rayons respectifs ? Justifier clairement la réponse.

Merci pour votre aide

Bonjour,

N'as-tu pas un schéma joint ?

A tout hasard je t'en mets un qui peut correspondre à la description de l'énoncé...

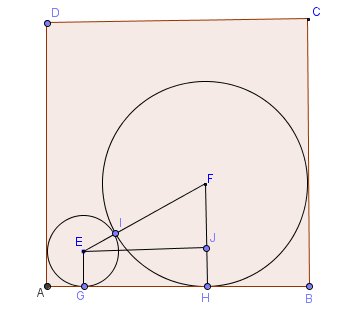
Merci de dire, si tu as un schéma, si celui-ci convient.

Si c'est bon, je t'indiquerai quelques pistes.

Oui, c’est un schema comme ca sauf qu’il n’a pas de triangle

D'accord.

J'ai construit le triangle car il est nécessaire aux calculs.
Si tu dois rendre cet exercice en devoir à la maison, il faudra que tu indiques la position des points utilisés.

Une piste possible,

Soit x le rayon du cochonnet.
Tu calcules toutes les longueurs utiles en fonction de x
Tu dois obtenir une équation d'inconnue x à résoudre
Ayant le rayon x du cochonnet, tu déduiras le rayon 4x de la boule.

Principe : AG+GH+HB=27

AG=x (rayon du cochonnet)
HB=4x (rayon de la boule)

d'où : x+GH+4x=27 <=> 5x+GH=27(équation ***)

Il faut trouver GH :

GH=EJ

Pour trouver EJ, utilise le théorème de Pythagore dans le triangle rectangle EJF (tu dois obtenir EI²=16x² d'où EJ=4x)

Au final, avec l'équation ***, tu dois trouver la valeur de x (rayon du cochonnet) et déduire celle de 4x (rayon de la boule)

Reposte si besoin.

Je n’arrive pas à résoudre l’équation, je ne sais pas comment faire

Il faudrait savoir où tu en es...

As-tu su appliquer le théorème de Pythagore pour obtenir EJ²=16x² ?

Non je ne l’ai pas fait je suis complètement perdue

Si ça t'arrange, je te détaille le début du calcul de EJ²

EJ²+JF²=EF² ( thorème de Pythagore)

EF=EI+IF=x+4x = 5x( somme des deux rayons)
FJ=FH-JH=FH-EG = 4x-x= 3x (différence des deux rayons)

Donc EF² = 25x²
Jf² = 9x²

Tu replaces dans la formule de pythagore écrite au début ed ctte réponse, ce qui donne :

EJ²+9x² = 25x²

En transposant 9x², tu obtiendras EJ²

En prenant ensuite la racine carrée , tu obtiendras EJ

Vu que EJ=GH, en remplaçant dans la formule *** de ma réponse précédente et en terminant la résolution, tu obtiendras x

Bons calculs . J'espère que tu va y arriver.

Reposte si tu as besoin d'une vérification de tes réponses.

Une remarque : je comprends que tu soit perdue !
Cet énoncé ne donne aucune indication . Il faut que tu trouves une marche à suivre seule...ce doit être cela l'esprit "Sangaku" !
S'il y avait plusieurs questions successives pour arriver au résultat final, ce serait infiniment plus facile...

OC= le rayon du cochonnet + rayon de la boule
Nous savons que le rayon de la boule = 4x
OC=x+4x
OC=5x

AC= rayon de la boule - rayon du cochonnet donc
AC=4x-x
AC=3x

Le triangle CAO est rectangle en A donc théorème de Pythagore
OA²+AC² = OC²
OA² + (3x)² = (5x)²
donc OA² = (5x)² - (3x²)
OA² = 25x²-9x² = (25-9)x² =16x²
Donc OA=V(16x²) ou V signifie racine carré de
OA = 4x

Le côté de la boite est égal à :
rayon du cochonnet + OA + rayon de la boule
x+4x+4x = 9x

Nous savons d'après l’énoncé que le côté de la boite est 27 cm
donc 9x=27
d'ou x=27/9 = 3

et 4x=4*3=12
Le rayon du cochonnet est de 3 cm et celui de la boule 12 cm

J'ai fait cela et j'aimerai savoir si mon résultat et juste

Tes résultats sont justes.

Une remarque : tes notations sont bizarres car elles ne correspondent pas à celles que j'ai indiquées dan le schéma joint...
J'imagine que tu as demandé de l'aide dans plusieurs forums et que tu as mélangé les notations ! ! !
Une prochaine fois, fais attention .

Merci beaucoup, oui j'ai demandé un peu d'aide

De rien !
A+