Équation d'une parabole passant deux points

Bonjour, j'ai un DM de maths à faire. Je dois déterminer l'équation d'une parabole passant par l'origine ainsi que par (20;26). J'ai réussi à trouver en bidouillant -0,065(x-0)(x-40) mais je cherche à prouver comment j'ai trouvé a (le coeff directeur). Quelqu'un pourrait m'aider où me donner un autre coeff directeur pour lequel ça fonctionne ?

Bonjour Rin,

Ta question n'est pas assez précise.
Par deux points passe une infinité de paraboles.
Peut-être s'agit-il d'une parabole d'axe (Oy) ou bien un autre point est donné ???

Merci de préciser.

@mtschoon non je n'ai pas plus de points, ce sont les seules conditions données sur le papier. Donc le prof à bien précisé qu'il y aurait plusieurs possible

D'accord.
Passant par deux points , tu auras donc une infinité de paraboles

Piste,
Equation : Pour $\ne 0$
$\fbox {y=ax^2+bx+c}$

La parabole passe par O(0,0)
En remplaçant x par 0 et y par 0, tu obtiens $c = 0$
d'où $\fbox{y=ax^2+bx}$

La parabole passe par A(20,26)
En remplaçant x par 20 et y par 26, après calculs et simplfications, tu dois obtenir $b = - 20 a + 1.3$

L'équation cherchée est donc : $\fbox{y=ax^2+(-20a+1.3)x}$

Pour chaque valeur non nulle de a, tu obtiens l'équation d'une parabole passant par O et A

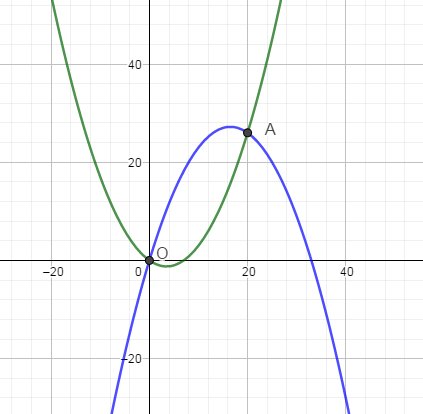
Pour illustration, je t'ai tracé deux de ces paraboles
la verte est obtenue avec a=0.1
La bleue est obtenue avec a=-0.1

Une remarque :
Ne parle pas de "coefficient directeur" lorsqu'il s'agit d'une parabole
Le coefficient directeur ne s'applique qu'aux droites vu qu'il indique la direction de la droite.
Pour une parabole, le coefficient a sert à sa concavité

@mtschoon oh merci beaucoup !

@mtschoon par contre comment tu as obtenu -20a + 1.3 ?

Je pense que tu parles de $b = - 20 a + 1.3$

Comme je te l'ai indiqué, dans $y=ax^2+bx$ , tu remplaces x par 20 et y par 26

Cela te donne d'abord $26=a(20^2)+b(20)$

Je te laisse terminer le calcul pour trouver b en fonction de a

@mtschoon lorsque je fais ce calcul je trouve

26 = a(20)^2 + b(20)
26 = 400a + 20b
26 - 400a = 20b
26 - 400/20a = 20b
26 - 20a = b

Je ne comprends pas comment continuer pour trouver b = -20a + 1.3

La 4ème ligne de ton calcul est bizarre...

Je reprends à partir du début du calcul :

Tu peux écrire, pour que ça soit plus simple

$a(20^2)+b(20)=26$
$400 a + 20 b = 26$
$20 b = - 400 a + 26$

Il te reste à diviser chaque membre par 20 pour obtenir b en fonction de a

@mtschoon ah j'ai vu mon erreur ! Merci !

De rien !

Bons calculs.