Dm maths médiane du triangle ABC

Bonjour, j'ai un devoirs maison à rendre et je bloque sur une partie de l'exercice, je sais pas comment je dois procéder, est-ce que je pourrais avoir un coup de pouce au moins que l'on me dit qu'elle méthode adopté, ca serait super.

Alors voilà l'exercice :

Dans un repère (O;I;J), on considère les points A(-1;4), B(-1;-1), C(5;1) et D(8;-8).

Montrer que le point D appartient à la médiane du triangle ABC issue de A.

Je sais que c'est sûrement avec cette propriété qu'il faut procéder :

Si dans un triangle, une droite est perpendiculaire à un
côté et passe par le sommet opposé à ce côté, alors
cette droite est une hauteur de ce triangle.

Voilà merci si vous répondez !

Bonjour vert31

Je comprends mal ta suggestion.
Tu veux travailler avec une médiane et tu parles de hauteur !

Je te joins un schéma pour éclairer la situation.
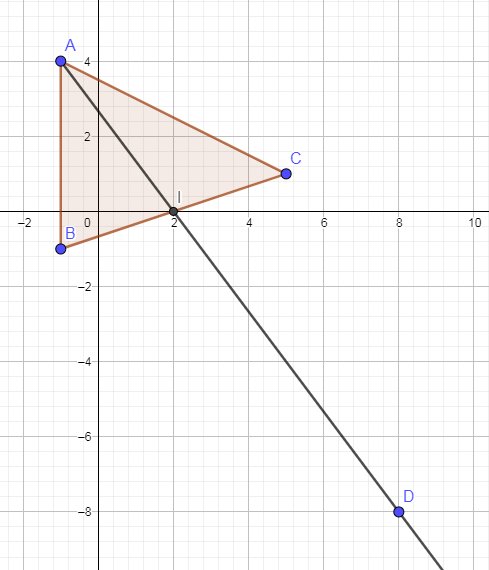
0_1538298151036_médiane.jpg

Piste :

Soit I le milieu de [BC]
$xI=xB+xC2x_I=\frac{x_B+x_C}{2}$
$yI=yB+yC2y_I=\frac{y_B+y_C}{2}$

Tu peux ainsi déterminer les coordonnées de I
La médiane est (AI)

Une méthode possible :
Tu peux trouver son équation (droite passant par deux points A et I)

Sauf erreur, cette équation peut s'écrire :
$y=−43x+83y=-\frac{4}{3}x+\frac{8}{3}$ ou si tu préfères $4 x + 3 y = 8$

Il te reste ensuite à vérifier que les coordonnées de D vérifient l'équation de (AI)

Bon travail.
Reposte si besoin.

Bonjour mtschoon

Ah oui effectivement je m'étais trompé de propriété merci !

C'est celle-ci :

Si dans un triangle une droite passe par un sommet et par le
milieu du côté opposé à ce sommet alors cette droite est une
médiane de ce triangle.

Je pense avoir trouvé, j'ai calculé les coordonnées de E et je trouve E(2;0) sachant qu'il est le milieu du segment [BC], donc E est une médiane du triangle ABC issue de A, et pour savoir si D est également une médiane je n'ai qu'a découvrir si [AE] et [ED] sont alignés, et si c'est bien le cas alors D est belle et bien une médiane appartenant au triangle ABC c'est bien ca ?

Ta nouvelle explication est bonne.
Oui , le milieu de [BC] a bien pour coordonnées (2,0)

Fait attention : D n'est pas une médiane...une médiane est une droite , ce n'est pas un point...
Oui, pour prouver que D est sur la médiane que tu appelles (AE), tu peux prouver que les points A, E, D sont alignés.

je te l'ai suggéré en passant par l'équation de la médiane, mais tu peux faire autrement en fonction de ton cours.
Par exemple, vecteurs colinéaires.

Merci beaucoup ! je vais changer ça.

Oui ça me semble plus facile avec la colinéarité.

Si la colinéarité des vecteurs fait partie de ton cours, la méthode est très bonne.