Fonctions polynômes (coût, recette, bénéfice)

Partie A
Un laboratoire pharmaceutique s'intéresse coût total de production d'un produit qu'il commercialise.
Ce coût exprime en euros est définie par:
$C(x)=13x3−11x2+100x+72C(x)=\frac{1}{3}x^3-11x^2+100x+72$ , où x représente la quantité de produit fabriqué en kilogramme.
Après une étude de marché le prix de vente du produit a été estimé 60€ le kg.
On donne ci-dessous les courbes représentatives des fonctions coût de produit et recette sur l'intervalle (5;30)

quelle courbe représente le coût total de production? La recette? Justifier
a) estimer pour quelle quantité le coût total de production et de 600 €
b) estimer la recette du laboratoire pour la vente de 15kg de produits
quelle quantité de produit le laboratoire doit-il vendre pour réaliser un bénéfice? Justifier

Partie B
Le bénéfice réalisé par l'entreprise est exprimé en euros par
$B(x)=−13x3+11x2−40x−72B(x)=-\frac{1}{3}x^3+11x^2-40x-72$ , avec $x∈[5,30]x\in[5,30]$

calculer B'(×)
en déduire les variations de la fonction B sur l'intervalle [5;30]
On considère que la production est entièrement vendue.
Déterminer la quantité à produire pour réaliser le bénéfice maximal
Quel est ce bénéfice?

(Formules re-écrites en Latex, pour plus de clareté)

Bonjour bibi38,

Ici, la convivialité et la politesse sont les bienvenues...
Il faudra y penser une autre fois si tu as besoin d'aide.

Je regarde la partie A.
Elle est exclusivement graphique.

Les énoncés doivent être écrits à la main, mais les graphiques scannés sans texte sont autorisés.
Ce serait bien de donner les courbes...

Je te joins un schéma pour x compris entre 5 et 30

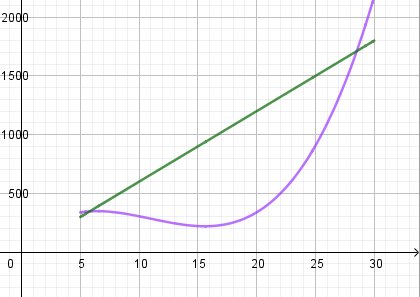
Le coût est représenté la portion de courbe d'équation $C(x)=13x3−11x2+100x+72C(x)=\frac{1}{3}x^3-11x^2+100x+72$
le prix de vente du produit a été estimé 60€ le kg donc la fonction recette est $R (x) = 60 x$ (fonction linéaire)

Tu dois ainsi pouvoir répondre à la 1.

Pour la 2 a), tu utilises la fonction "Coût"
Tu lis l'abscisse du point d'ordonnée 600

Pour la 2 b), tu utilises la fonction "Coût"
Tu lis l'ordonnée du point d'abscisse 15

Pour la 2 c), la recette R(x) doit être supérieur au coût C(x)
Tu utilises les deux fonctions pour lire la réponse.

Tiens nous au courant de tes réponses si tu as besoin d'une vérification.

Complément pour consultation, car cet exercice n'a pas vraiment été étudié, la partie A étant composée seulement de lectures graphiques.

Pistes de la partie B

$B(x)=R(x)−C(x)=−13x3+11x2−40x−72B(x)=R(x)-C(x)=-\frac{1}{3}x^3+11x^2-40x-72$

Avec les formules usuelles
$B′(x)=−13(3x2)+11(2x)−40=−x2+22x−40B'(x)=-\frac{1}{3}(3x^2)+11(2x)-40=-x^2+22x-40$

$B^{'} (x)$ est un polynôme du second degré dont on doit étudier le signe

Sur R, les solutions de $B^{'} (x) = 0$ sont $x = 2$ et $x = 20$
B'(x) est strictement positif sur $] 2, 20 [$ et strictement négatif sur $]−∞,2[U]20,+∞[]-\infty,2[ U ]20,+\infty [$

On restreint l'étude à l'intervalle $[5, 30]$ pour trouver les variations de B sur cette intervalle et le maximum

B croissante sur [2,20]
B a un maximum pour x=20
B décroissante sur [20,30]

Pour $x = 20$ $\approx 861.33$ €