Prouve que f accepte une valeur maximale absolue sur IR+

Bonjour à tous et à toutes!
Je trouve une grande difficulté à résoudre cette question

soit f une fonction positive et continue sur IR+ telle que $lim⁡x→+∞f(x)=0\displaystyle \lim _{x\to +\infty}f(x)=0$
Prouve que f accepte une valeur maximale absolue sur IR+, ça veut dire:
Existe c appartient à IR+ tel que
Quelque soit x appartient à IR+ ; $\le f(c)$

Bonjour,

J'essaie de te donner des indications, mais je ne sais pas exactement la définition de limite de ton cours...alors, il faudra adapter...

Je suppose que f n'est pas constamment nulle .
Dans ce cas , c serait n'importe quelle valeur de R+

Si f n'est pas constamment nulle, il existe une valeur $x_1$ de R+ telle que $f(x1)>0f(x_1) \gt 0$

En utilisant la définition usuelle de limite , $lim⁡x→+∞f(x)=0\displaystyle \lim_{x \to +\infty} f(x)=0$ se traduit par :
Pour tout $ϵ>0\epsilon \gt 0$ , il existe B de R+ tel que : $x>Bx\gt B$ => $\lt \epsilon$

Tu prends $ϵ=f(x1)\epsilon=f(x_1)$ , et tu peux déduire que sur $]B,+∞[]B,+\infty [$ $\lt f(x_1)$ ,
$f(x_1)$ est donc maximum relatif sur $]B,+∞[]B,+\infty [$

Sur $[0, B$ ], vu que f est continue ( et que l'image d'un segment est un segment), tu peux déduire que f admettra un maximum relatif $f(x_2)$

Tu tires la conclusion pour c :
Suivant que $f(x_1)$ est supérieur ou inférieur à $f(x_2)$ , le maximum absolu sera $f(x_1)$ ou $f(x_2)$ (donc c sera $x_1$ ou $x_2$ )

Mercii @mtschoon
Est-ce-que vous pouvez m'expliquer la dernière partie, je veux bien la comprendre.

Indique ce que tu appelles la "dernière partie".
Tu parles de l'intervalle [0B] ou de la conclusion ?

@mtschoon je parle de l'intervalle [0,B]

D'accord.
Je te mets un schéma pour éclairer.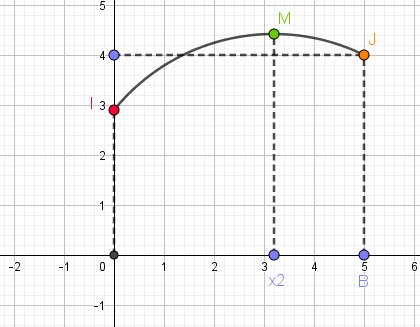

Je te donne une explication "concrète"

f est continue sur [0B]
La représentation graphique de f , sur [0B], sera une courbe continue de point de départ I et de point d'arrivée J
Il y aura nécessairement une maximum $f(x_2)$ correspondant au point M sur le schéma
Remarque : il y aura aussi un minimum (qui correspond au point I son mon schéma, vu la courbe que j'ai tracé)