Développements limités (DL d'un quotient)

Re-bonjour,
Nous avons fait vendredi un exercice sur les développements limités. Je n'ai pas compris la méthode utilisée pendant le TD.
Est-il possible de me réexpliquer la démarche?
par exemple pour $ex−1cosx\displaystyle \frac{e^x-1}{cosx}$ en 0 à l'ordre 3.

Merci par avance

Bonjour dut,

Peux tu indiquer la méthode utilisée en TD ?

Bonjour Dut et Noemi,

Effectivement, Dut, il faudrait connaître la méthode utilisée en TD, mais comme tu ne l'as pas comprise cela va être dur de nous l'expliquer...

Je tente de t'indiquer la méthode usuelle.
Demande en détaillant le mieux possible si elle ne te convient pas.

Tu dois avoir un formulaire des DL usuels au voisinage de 0
Ici, tu as besoin des DL de $e^x$ , de $c o s x$ et de $11−x\frac{1}{1-x}$
Regarde ton cours sur ce sujet.

$ex=1+x+x22+x36+o(x3)e^x=1+x+\frac{x^2}{2}+\frac{x^3}{6}+o(x^3)$

Remarque : $o(x^3)$ est le "reste" du DL.
le "o"veut dire que ce reste en négligeable par rapport à $x^3$ au voisinage de 0.
Cela doit être expliqué dans ton cours.

Donc:
$\fbox{e^x-1=x+\frac{x^2}{2}+\frac{x^3}{6}+o(x^3)}$

$\fbox{cosx=1-\frac{x^2}{2}+o(x^3)}$
(il n'y a pas de terme en $x^3$ dans le DL de $c o s x$ )

$\displaystyle \fbox{\frac{e^x-1}{cosx}=(e^x-1)\times \frac{1}{cosx}}$

Il faut que tu cherches le DL de $1cosx\frac{1}{cosx}$ et ensuite tu feras le produit des deux DL (celui de $e^x-1)$ et de $1cosx\frac{1}{cosx}$ )

Recherche du DL de $1cosx\frac{1}{cosx}$

$cosx=1−x22+o(x3)cosx=1-\frac{x^2}{2}+o(x^3)$
donc
$1cosx=11−x22+o(x3)\frac{1}{cosx}=\frac{1}{1-\frac{x^2}{2}+o(x^3)}$

Tu poses
$X=x22+o(x3)X=\frac{x^2}{2}+o(x^3)$

(remarque : $o(x^3$ ) et $o(x^3$ ) ont la même signification)

donc $1cosx=11−X\frac{1}{cosx}=\frac{1}{1-X}$

Tu prends le DL de $11−X\frac{1}{1-X}$
$\fbox{\frac{1}{1-X}=1+X+X^2+o(X^2)}$
donc
$1cosx=1+x22+x44+o(x4)\frac{1}{cosx}=1+\frac{x^2}{2}+\frac{x^4}{4}+o(x^4)$

Vu que tu cherches un DL d'ordre 3, tu peux réduire:
$\fbox{\frac{1}{cosx}=1+\frac{x^2}{2}+o(x^3)}$

Multiplication du DL de $e^x-1)$ avec le DL de $1cosx\frac{1}{cosx}$

$(ex−1)×1cosx=(x+x22+x36+o(x3))×(1+x22+o(x3))(e^x-1)\times \frac{1}{cosx}=\biggl(x+\frac{x^2}{2}+\frac{x^3}{6}+o(x^3)\biggl)\times\biggl(1+\frac{x^2}{2}+o(x^3)\biggl)$

Tu développes.
Comme tu cherches un DL d'ordre 3, tu n'as pas besoin d'écrire les termes de degré supérieur à 3

Il doit te rester

$(ex−1)×1cosx=x+x32+x22+x36+o(x3)(e^x-1)\times \frac{1}{cosx}=x+\frac{x^3}{2}+\frac{x^2}{2}+\frac{x^3}{6}+o(x^3)$

En réduisant et ordonnant
$(ex−1)×1cosx=x+x22+4x36+o(x3)(e^x-1)\times \frac{1}{cosx}=x+\frac{x^2}{2}+\frac{4x^3}{6}+o(x^3)$

En simplifiant
$(ex−1)×1cosx=x+x22+2x33+o(x3)(e^x-1)\times \frac{1}{cosx}=x+\frac{x^2}{2}+\frac{2x^3}{3}+o(x^3)$

CONCLUSION
$\fbox{\frac{e^x-1}{cosx}=x+\frac{x^2}{2}+\frac{2x^3}{3}+o(x^3)}$

Bonne lecture !

Bonjour Mtschoon, Bonjour Noemi,
La méthode utilisée durant le TD était de dériver, par exemple pour tan(x) en PI à l'ordre 3, 3 fois tan(x).
Merci pour cette méthode qui est vraiment beaucoup plus simple et surtout que je penses avoir compris à la première lecture.
C'est la première fois que je fais des DL (c'est un rajout par rapport à l'année dernière).
Je bloque néanmoins sur une des dernières étapes et comme souvent sur un produit. Je n'arrive pas à trouver juste le resultat correspondant à la ligne ci dessous. Pour les lignes d'après ces bon en considérant votre réponse que je n'arrive pas à prouver.

@mtschoon a dit dans Développements limités (DL d'un quotient) :

Il doit te rester

$(ex−1)×1cosx=x+x32+x22+x36+o(x3)(e^x-1)\times \frac{1}{cosx}=x+\frac{x^3}{2}+\frac{x^2}{2}+\frac{x^3}{6}+o(x^3)$

De plus dans le formulaire des DL j'ai pour cos:
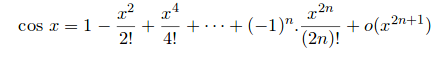
0_1540046707504_5d6c47da-934f-4d04-b3e1-070f2a5baf4c-image.png

Pourquoi dans la démonstration que vous m'avez faite $o(x^3$ ) ,si je comprends le document o(x^(2*n+1)) avec n=3 ferait o(x^5)

Merci encore pour l'explication de qualité

Bonjour Dut,

Très contente que la méthode te convienne.
J'essaie de répondre à tes questions

Pour le produit, c'est toujours la propriété de distributivité de la multiplication par rapport à l'addition
Rappel :
(a+b+c)(e+f)=ae+af+be+bf+ce+cf

Ici, sauf erreur, tu trouves
$x.1+x.x22+x22.1+x22.x22+x36.1+x36.x22\displaystyle x.1+x.\frac{x^2}{2}+\frac{x^2}{2}.1+\frac{x^2}{2}.\frac{x^2}{2}+\frac{x^3}{6}.1+\frac{x^3}{6}.\frac{x^2}{2}$

Tu réduis en utilisant les propriétés des puissances : $x^m.x^n=x^{m+n}$

Ainsi tu obtiens:
$x+x32+x22+x44+x36+x512\displaystyle x+\frac{x^3}{2}+\frac{x^2}{2}+\frac{x^4}{4}+\frac{x^3}{6}+\frac{x^5}{12}$

Comme tu cherches un DL d'ordre 3, tu négliges les termes dont l'exposant de x dépasse 3

Il te reste donc

$x+x32+x22+x36\displaystyle x+\frac{x^3}{2}+\frac{x^2}{2}+\frac{x^3}{6}$

J'essaie de t'expliquer le $o(x^{2n+1})$ (pas facile...)

La formule de ton formulaire est tout à fait exacte.
(J'ai repris cette version dans mes réponses précédentes, pour ne pas te perturber.
Avant que tu l'écrives, je ne savais pas la version...)

De façon générale, lorsqu'un DL s'arrête à un ordre n, le "reste non écrit" est un infiniment petit négligeable par rapport à $x^n$ et se note $o(x^n)$
Certains formulaires l'appliquent ainsi dans tous les cas (c'est le plus simple)

Certains donnent une meilleure précision pour le cas où le développement est constitué exclusivement de termes en x à une puissance paire, ou de termes en x à une puissance impaire.
C'est le cas de ton formulaire pour cosx

Le développes de cosx est $1−x22+x424−...+...1-\frac{x^2}{2}+\frac{x^4}{24}-...+...$

Vu qu'il n'y a de termes en $x^3$ , on peut écrire le DL d'ordre 2 :
$1−x22+o(x2)1-\frac{x^2}{2}+o(x^2)$
Mais on peut faire plus précis en indiquant que le terme en $x^3$ est nul, et écrire :
$cosx=1−x22+0.x3+o(x3)cosx=1-\frac{x^2}{2}+0.x^3+o(x^3)$
D'où
$cosx=1−x22+o(x3)cosx=1-\frac{x^2}{2}+o(x^3)$

le $o(x^5)$ que tu proposes en faux

Regarde la formule de ton formulaire

$\fbox{cosx=1-\frac{x^2}{2!}+\frac{x^4}{4!}+...+(-1)^n\frac{x^{2n}}{(2n)!}+o(x^{2n+1})}$

Il faut bien l'interpréter.
Regarde bien la fin de la formule (après les ...)

Vu que tu dois t'arrêter à l'ordre 3 ( et qu'il n'y a pas de terme en $x^3$ , il faut s'arrêter à l'ordre 2 c'est à dire prendre n=1

Ainsi, pour $n=1\fbox{n=1}$
$...+(−1)nx2n(2n)!+o(x2n+1)=...+(−1)1x2.12.1)!+o(x2.1+1)...+(-1)^n\frac{x^{2n}}{(2n)!}+o(x^{2n+1})=...+(-1)^1\frac{x^{2.1}}{2.1)!}+o(x^{2.1+1})$ $

c'est à dire:

$...+(−1)nx2n(2n)!+o(x2n+1)=...−x22+o(x3)...+(-1)^n\frac{x^{2n}}{(2n)!}+o(x^{2n+1})=...-\frac{x^{2}}{2}+o(x^{3})$

et au final

$\fbox{cosx=1-\frac{x^{2}}{2}+o(x^{3})}$

Prends le temps (il t'en faudra...) de regarder tout ça de près mais expliquer sur un forum ( et en Latex) ce n'est vraiment pas facile.
Dans une classe avec un tableau, c'est plus simple...

Bonne lecture et bon travail.

Bonjour Mtschoon,
Merci pour l'explication c'est beaucoup plus clair maintenant. Je vais faire d'autres exercices types pour vérifier la bonne compréhension de la méthode.
J'ai pris RDV jeudi matin avec mon enseignante de Maths afin de faire le point sur mes difficultés et peut être envisager des solutions pour m'aider.
Bonne journée

Bon travail Dut .

Effectivement, si une solution d'aide pouvait t'être trouvée, ce serait parfait pour toi.
Dans tous les cas, tu peux compter sur nous, bien sûr. On fait au mieux !

Bonne journée !