Probabilité (devoir)

Bonjour,
J'ai un devoir à faire mais je ne comprends pas trop, voici l'énoncé :

Une étude du ministère de l’Éducation Nationale, portant sur les résultats au baccalauréat en 2012
dans l’académie de Bordeaux montre que :
• 13 796 candidats ont obtenu un baccalauréat général, ce qui représente un taux de réussite de
90,4 % ;
• 6 327 candidats se sont présentés à un baccalauréat technologique. 5 492 ont été reçus ;
• 12 124 candidats se sont présentés à un baccalauréat professionnel. Le taux de réussite a été
de 82,3 % .
Dans cet exercice, les probabilités seront arrondies au millième près.

PARTIE A :

On choisit au hasard un candidat ayant obtenu un baccalauréat dans l’académie de Bordeaux
en 2012.
On note les événements :
• G : « le candidat a obtenu un baccalauréat général »
• T : « le candidat a obtenu un baccalauréat technologique »
• P : « le candidat a obtenu un baccalauréat professionnel ».
Déterminer la probabilité de chacun des événements G, T et P.
On choisit au hasard et de manière indépendante deux personnes ayant obtenu un
baccalauréat en 2012 dans l’académie de Bordeaux.
a) Construire un arbre pondéré traduisant la situation.
b) Calculer la probabilité p1 que les deux personnes aient obtenu un baccalauréat d’une
série identique.
c) Calculer la probabilité p2 qu’un seul des deux candidats ait obtenu un baccalauréat
professionne

Merci d'avance

Partie A :
1)
P(G) = 0.90
P(T) = 0.88
P(P) = 0.82

Je ne suis pas sûr.

Bonsoir Chrosmiq75,

Revois tes calculs.
On choisit un candidat parmi tous les candidats qui ont obtenu un baccalauréat.

@noemi a dit dans Loi binomiale (devoir) :

Bonsoir Chrosmiq75,

Revois tes calculs.
On choisit un candidat parmi tous les candidats qui ont obtenu un baccalauréat.

Je ne sais pas comment faire,...
1/90.4 ?

@chrosmiq75,

Calcule le nombre total de candidat qui ont eu un baccalauréat.

@noemi a dit dans Loi binomiale (devoir) :

@chrosmiq75,

Calcule le nombre total de candidat qui ont eu un baccalauréat.

32247

@chrosmiq75,
En fait non
c'est 13796 + 5492 + 12124x0,823 = .....
....

@noemi a dit dans Loi binomiale (devoir) :

@chrosmiq75,
En fait non
C'est 13796 + 5492 + 12124x0,823
....

P(G) = 13796/32247 = 0.428
P(T) = 5492 / 32247 = 0.170
P(P) = 12124 / 32247 = 0.376
?

@chrosmiq75,
Rectifie tes calculs le total était faux c'est 29266, il faut prendre en compte le nombre de candidats qui ont réussi.

@noemi a dit dans Loi binomiale (devoir) :

@chrosmiq75,
En fait non
c'est 13796 + 5492 + 12124x0,823 = .....
....

Pourquoi x0.823?

@chrosmiq75

Le taux de réussite est de 82,3 % et tu calcules le nombre de candidats du baccalauréat professionnel qui ont réussi.

@noemi Je ne comprends pas ..

Bonjour Chrosmiq75,

Précise la partie que tu ne comprends pas.
Il faut connaitre le nombre de candidats admis :
13 796 candidats ont obtenu le baccalauréat général
5 492 candidats ont obtenu le baccalauréat technologique
12 124 x 82,3% ont obtenu le baccalauréat professionnel

le nombre total de candidats ayant eu un baccalauréat :
13 796 + 5 492 + ..... = .......

Je te laisse compléter les .....

13 796 + 5 492 + 9978 (12 124 x 0.823) = 29266

P(G) = 13796 / 29266 = 0.471
P(T) = 5492 / 29266 = 0.188
P(P) = 9978 / 29266 = 0.341

Une erreur d'arrondi pour P(T) = 0,188 et P(P) = 0,341.

Pour la question 2, Construis un arbre pondéré et calcule la probabilité pour chaque cas.

Ce message a été supprimé !

Comme ceci ?

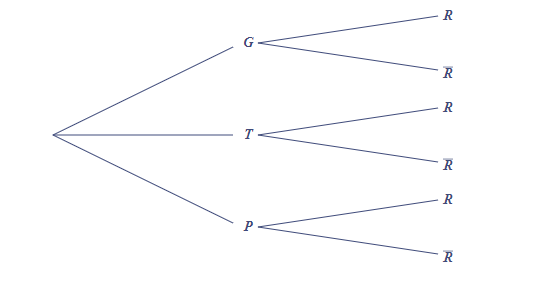
Le début est juste, pour la deuxième partie à chaque cas, il faut associer les trois possibilités G, T et P.

Par exemple pour la branche G, il faudrait rajouter G - T - P puis a chaque nouvelle branche R et R barre?

A chaque branches tu rajoutes G, T et P

@noemi a dit dans Loi binomiale (devoir) :

A chaque branches tu rajoutes G, T et P

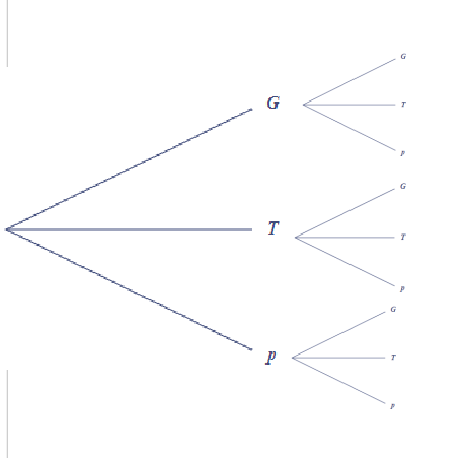
(Désolé si c'est mal fait à l'ordinateur)

C'est juste.

Tu peux calculer pour chaque branche la probabilité correspondante.

ça ?

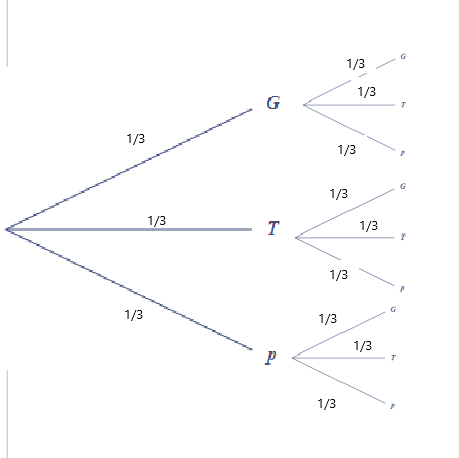
Non,

Tu prends les valeurs de P(G), P(T) et P(P) que tu as trouvées à la question précédente.

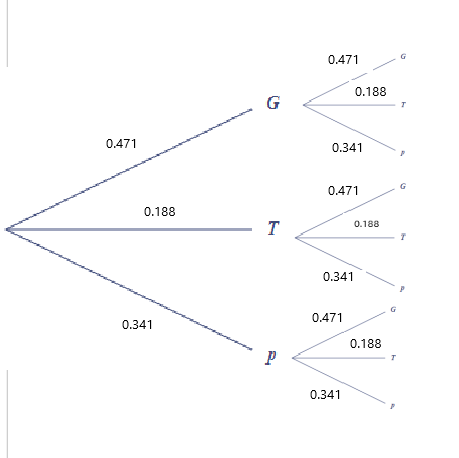
Ceci?

C'est correct.

Pour le 2) a et b comment faire ?

Pour la question b) tu prends sur les branches qui indiquent le même bac (Exemple GG, ...) et tu calcules la probabilité correspondante puis tu additionnes les probabilités.
Pour la question c) tu prends les branches qui contiennent une seule fois P et tu appliques le même raisonnement que pour la question b).

b) P(GG) = 0.471+0.471 = 0.942
P(TT) = 0.188+0.188 = 0.376
P(PP) = 0.341 + 0.341 = 0.682
P(GG) + P(TT) + P(PP) = 2 ?

Il ne faut pas additionner les probabilités mais les multiplier
P(GG) = 0,471 x 0,471 = ....
....

@chrosmiq75 a dit dans Loi binomiale (devoir) :

P(GG) = 0.471+0.471 = 0.942
P(TT) = 0.188+0.188 = 0.376
P(PP) = 0.341 + 0.341 = 0.682
P(GG) + P(TT) + P(PP) = 2 ?

P(GG) = 0.471x0.471 = 0.221
P(TT) = 0.188x0.188 = 0.035
P(PP) = 0.341x0.341 = 0.116
P(GG) + P(TT) + P(PP) = 0.372

c)
P(GP) = 0.471 x 0.341 = 0.160
P(TP) = 0.188 x 0.341 = 0.064
P(PG) = 0.341 x 0.471 = 0.160
P(PT) = 0.341 x 0.188 = 0.064

P(GP) + P(TP) + P(PG) + P(PT) = 0.488

Attention à l'arrondi, P(GG) = 0,222.
P(GP) = P(PG) = 0,161

Refais les sommes.

b)
P(GG) = 0.471x0.471 = 0.222
P(TT) = 0.188x0.188 = 0.035
P(PP) = 0.341x0.341 = 0.116
P(GG) + P(TT) + P(PP) = 0.373

c)
P(GP) = 0.471 x 0.341 = 0.161
P(TP) = 0.188 x 0.341 = 0.064
P(PG) = 0.341 x 0.471 = 0.161
P(PT) = 0.341 x 0.188 = 0.064
P(GP) + P(TP) + P(PG) + P(PT) = 0.45

Les résultats sont justes.

Merci à vous,
j'ai une seconde partie dans le devoir, êtes-vous encore disponible pour de l'aide?

Oui,

Si c'est sur un autre thème propose un nouveau sujet.

C'est le même thème,
Voici la partie :

Calculer la probabilité p qu’un candidat choisi au hasard ait obtenu le baccalauréat en 2012
dans l’académie de Bordeaux.
On choisit, au hasard et de manière indépendante, 5 candidats au baccalauréat en 2012 dans
l’académie de Bordeaux.
On note X la variable aléatoire égale au nombre de candidats ayant obtenu le baccalauréat.
a) Quelles sont les valeurs prises par X ?
b) Montrer que X suit une loi binomiale dont on précisera les paramètres.
c) Calculer la probabilité que tous les candidats, parmi les cinq choisis, aient été reçus.
d) Calculer la probabilité que trois candidats, parmi les cinq choisis, aient obtenu le
baccalauréat en 2012.
e) Calculer la probabilité qu’au moins un candidat, parmi les cinq choisis, ait obtenu le
baccalauréat en 2012.

Pour la 1. j'ai fait ceci mais je ne suis pas sûr :
(12471+5492+9978) / 29266 = 0.955
La probabilité qu’un candidat choisi au hasard ait obtenu le baccalauréat en 2012
dans l’académie de Bordeaux est de 0.955

Pour la question 1, il faut diviser le nombre total de candidats ayant eu le bac par le nombre total de candidats qui ont passé le bac.
Calcule d'abord le nombre de candidats au bac général, puis le nombre total de candidats au bac.

Il y a 15121 candidats pour le bac général?
13796 x 0.904 = 12471
13796 - 12471 = 1325
13796 + 1325 = 15121

Non,

Pour le bac général c'est n = 13796 / 0,904 = ....
car n x 0,904 = 13 796.

Donc 15261 ?

Oui 15261 candidats pour le bac général.

Alors
(13796+5492+9978) / 33712 = 0.87

C'est correct.
Tu as arrondi au centième, c'est indiqué dans l'énoncé ?

@noemi
Le resultat trouvé sur la calculatrice est 0.8681181775
Je dois arrondir au millième donc 0.868?

Oui au millième 0,868

On choisit, au hasard et de manière indépendante, 5 candidats au baccalauréat en 2012 dans
l’académie de Bordeaux.
On note X la variable aléatoire égale au nombre de candidats ayant obtenu le baccalauréat.

a) Quelles sont les valeurs prises par X ?
X = 1 : 0.868 ?

X correspond au nombre de candidat ayant obtenu le baccalauréat donc
0, ou 1, ou ....
X = {0 ; 1; 2; 3; 4; 5 }

Je ne comprends pas ?

On choisit au hasard 5 candidats au baccalauréat en 2012,
Les issues possibles sont soit admis soit refusés au Bac;
Sur les 5 candidats, les possibilités sont :
soit 0 admis;
soit 1 admis;
soit 2 admis;
.....
Donc X = ....

X = 0,1,2,3,4,5 ?

Oui
X = {0; 1; 2; 3; 4; 5}

b) Montrer que X suit une loi binomiale dont on précisera les paramètres.

L'expérience consistant à choisir un candidat au bac de 2012 et constater s'il a le bac, l'expérience a deux issues possibles :

Le succès (le candidat a obtenu le bac) avec la probabilité p = 0.868
L'échec (le candidat n'a pas obtenu le bac) avec la probabilité q = 1-p = 0.132
Cette expérience est donc une épreuve de Bernoulli.

On repete cette expérience de façon identique et indépendante 5 fois donc n= 5
Donc X suit la loi binomiale de paramètre n = 5 et de probabilité = 0.868

c) Calculer la probabilité que tous les candidats, parmi les cinq choisis, aient été reçus.
P(X=5) = 0.493
( BinomialPD (5,5,0.868) )

d) Calculer la probabilité que trois candidats, parmi les cinq choisis, aient obtenu le
baccalauréat en 2012.
P( $\leq 3$ ) = 0.132
( BinomialCD (3,5,0.868)

e) Calculer la probabilité qu’au moins un candidat, parmi les cinq choisis, ait obtenu le
baccalauréat en 2012.

P(X $≥1\geq 1$ ) =1 - P( $\leq 0$ ) = ??? (Je ne sais pas comment faire du coup)

Je me suis trompé pour la d) c'est P(X=3) = 0.114

Bonjour Chrosmiq75,

Les questions c) et d) sont justes.
Pour la question e) c'est :
P(X $≥1\geq 1$ ) =1 - P( $X = 0$ ) =.......
L'événement contraire étant 0 candidat a eu le bac.

Bonjour,
P(X $≥1\geq 1$ ) =1 - P(X=0) = 0.999

Le résultat est 0,999959.... donc voisin de 1.

J'arrondi donc à 1?

S'il est précisé arrondir au millième, cela fait 1, donc tu peux conclure que si on choisit 5 candidats au hasard, au moins 1 a eu le bac.

Ok, merci beaucoup pour votre aide et votre patience !

Bon travail, tu as suivi mes conseils. J'espère que tu as tout compris.

Oui j'ai reussi a comprendre au fur et à mesure

Ok, c'est bien.