barycentre :ligne de niveau

[koned]

ABC triangle. AB=5 ;BC=7 et AC=4
G=bar{(A, 2) ;( B, 3) ;( C, 1) }

Construit l ensemble des points M dans chacun des cas tels que

• 2MA² +3MB²=BC²

• 2MA²+MC²=AC²

• 3MB² +MC²=19

• MA÷MB =2

• MB÷MC=3/4

[mtschoon]

koned, bonjour,

Ce serait bien que tu prennes l'habitude de donner quelques signes de convivialité .
Un petit "bonjour", "merci" font plaisir aux personnes qui apportent de l'aide...

Je ne sais pas si ton énoncé est entier, mais ce n'est pas le point G qui sert directement dans les questions posées.
Vu qu'il s'agit de constructions, tu peux commencer par placer le point G en utilisant la propriété d'associativité des barycentres.

$G_1=Barycentre(A,2),(B,3)$
$G_2=Barycentre(A,2),(C,1)$
$G_3=Barycentre(B,3),(C,1)$
Ainsi G est le point d'intersection des droites $(C{G}_1),(B{G}_2),(A{G}_3)$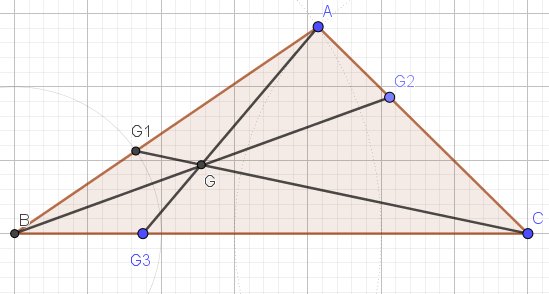

Pour ta première question, tout dépend de ton cours

Si tu sais que $aM{A}^2+bM{B}^2=(a+b)(M{G}_1{)}^2+a(G_{1}A{)}^2+b(G_{1}B{)}^2$
Ici $a=2$ et $b=3$
Tu utilises cette formule.

Sinon, tu la prouves avec la relation de Chasles, mais c'est plus long.