Est-ce que f est dérivable?

Bonjour à tous les membres et bon weekend!
Je veux poser une question, c'est que je trouve toujours que les fonctions avec la valeur absolue sont difficiles pour moi
Par exemple: est ce que $f$ est dérivable en 1 (je sais qu'on doit calculer la limite quand x tend vers 1 de ${(f(x)-f(1))}/{(x-1)}$ mais quand je veux la calculer je me bloque! A-t-il quelques astuces ou méthode? !

$f(x)=x∣x−1∣+2x+1\displaystyle f(x)=\frac{x|x-1|+2}{x+1}$

(formule re-écrite en Latex)

Re-bonjour Mathématicienne,

Je n'ai absolument pas regardé de près ( je regarderai plus tard)

Principe :

f(1)=1

Pour $x≥1x\ge 1$ , |x-1|=x-1 .
Tu déduis l'expression de f(x) dans ce cas et tu calcules le nombre dérivé à droite (en passant par le taux).

Pour $x≤1x\le 1$ , |x-1|=-x+1 .
Tu déduis l'expression de f(x) dans ce cas et tu calcules le nombre dérivé à gauche (en passant par le taux)

Si tu trouves pareil, f sera dérivable en x=1, sinon elle ne le sera pas.

Après calculs, tu dois trouver :
nombre dérivé à gauche $A_1=-1$
nombre dérivé à droite $A_2=0$

Donc f non dérivable pour x=1

Regarde la représentation graphique de f
Je n'ai pas tracé les deux demi-tangentes, ce que tu peux faire, au point (1,1), mais la courbure au voisinage de x=1 permet de deviner les réponses.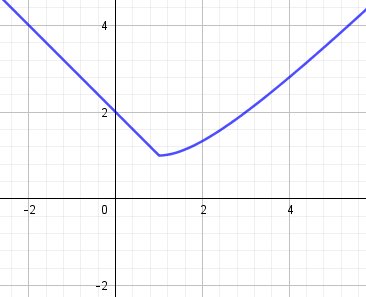

Reposte si besoin.

On peut clairement remarquer à partir de la représentation graphique que la fonction n'est pas dérivable en 1.
Maintenant c'est clair, j'ai trouvé les mêmes solutions pour A1 et A2.
Merciii infiniment !

Et si on a la partie entière, Comment ça va être ?

Même démarche pour la partie entière E

Dérivabilité pour x=1 ?

E(1)=1
Pour $x∈[1,2[x\in [1,2[$ E(x)=1
Pour $x∈[0,1[x\in[0,1[$ E(x)=0

Après calculs par le taux :

Pas de nombre dérivée à gauche car le taux tend vers l'infini
Nombre dérivé à droite = 0

E est non dérivable pour x=1 (seulement dérivable à droite)

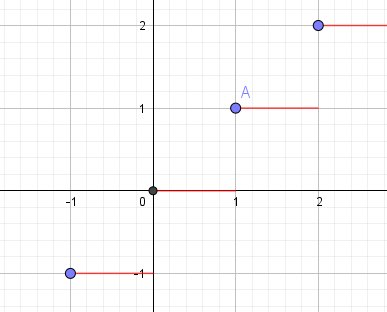
Sur la courbe, en A, il y a, si on la trace, une demi-tangente horizontale à droite (évident).
Par la gauche, on pourrait"presque penser" à une demi-tangente "verticale" mais comme il n'y a pas continuité, c'est à exclure...

C'est compris!
Merciiiii

De rien ! A+