Etude de fonction, TVI, Algorithme pour dichotomie.
-
Mmathiques dernière édition par mtschoon
Soit g la fonction définie sur [1 ; 4] par g(x)=x^3 -1-1/x
- Dresser le tableau de variations de g .
- Étudier le nombre de solutions de l’équation g(x)=10 . Justifier.
Je ne suis pas sur de mes résultats g'(x)=3x^2+1/x^2 ?
-
Bonjour mathiques,
La dérivée est juste.
Etudie son signe pour dresser le tableau de variation.
-
?Un Ancien Utilisateur dernière édition par
-
Mmathiques dernière édition par
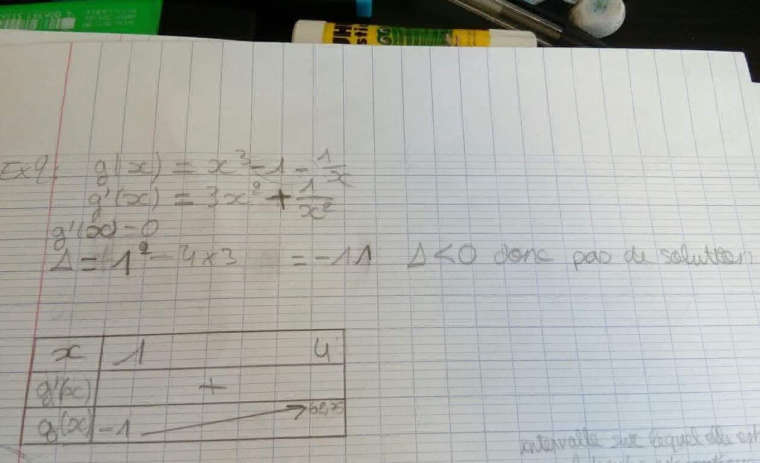
voici le tableau de signe c'est chrosmique75 qui la envoyé car je n'y arrivait pas
-
La résolution de g'(x) = 0 est fausse.
g'(x) est la somme de termes aux carrés donc g'(x) .....
-
Mmathiques dernière édition par
Je ne comprend pas il ne faut pas faire Delta??
-
Delta s'applique avec une équation du second degré,
ici c'est 3x2+1x23x^2 + \dfrac{1}{x^2}3x2+x21,
Pour x>0x\gt0x>0 ; 3x23x^23x2 > 0 et 1x2\dfrac{1}{x^2}x21 > 0 donc
3x2+1x23x^2 + \dfrac{1}{x^2}3x2+x21 .......
La dérivée est donc ........
et la fonction ........
-
Mmathiques dernière édition par
@noemi
3x^2+1/x^2 > 0 ?
-
mtschoon dernière édition par mtschoon

Bonjour Noemi et matiques,
@mathiques ,
Si ça peut te faire gagner du temps (en attendant que Noemi te répondre), la réponse est OUI (pour x compris entre 1 et 4)
-
Mmathiques dernière édition par
bonjour @mtschoon merci de ton aide je suis perdu je ne comprend plus grand chose..
-
mtschoon dernière édition par mtschoon

Détaille ce que tu ne comprends pas, pour que l'on puisse t'aider plus.
Si c'est le signe de g'(x) qui te pose toujours problème, j'explicite un peu.
Pourx∈[1,4]x \in[1,4]x∈[1,4], x est strictement positif
Lorsqu'on l'élève au carré, x2x^2x2 est strictement positif
Lorsqu'on multiplie par 3, 3x23x^23x2 est strictement positifDe même, en prenant l'inverse de x2x^2x2, 1x2\frac{1}{x^2}x21 est strictement positif
La somme de deux nombres strictement positifs est strictement positive donc
la somme 3x2+1x23x^2+\frac{1}{x^2}3x2+x21 est strictement positiveConclusion :
Pour x∈[1,4]x \in[1,4]x∈[1,4] , la dérivée est strictement positive donc g strictement croissante.Le tableau de variation que tu donnes est juste mais c'est l'explication relative à g'(x) qui est mauvaise.
Comme te l'a dit Noemi, g'(x) n'est pas un polynôme du second degré
Pour a différent de 0, un polynôme de second degré s'écrit $\fbox{ax^2+bx+c}$
Il n'y a pas de xxx , ni de x2x^2x2, au dénominateur, dans un polynôme du second degré.
Or ici, il y a x2x^2x2 au dénominateur. donc g'(x) n'est pas un polynôme du second degré donc les formules sur Δ\DeltaΔ ne peuvent pas s'appliquer.Il faut raisonner directement, comme indiqué .
Reposte si besoin.
-
Mmathiques dernière édition par mtschoon
@mtschoon Je pense avoir compris maintenant vu que ce n'est pas une fonction polynôme de second degré il ne faut pas que je calcul delta.
J'applique alors directement mon tableau avec g strictement croissante.
Mon tableau est-il bon?
-
Bonjour mathiques,
Le tableau de variations est juste.
Tu peux résoudre la question 2 en utilisant le théorème des valeurs intermédiaires.
-
Mmathiques dernière édition par
@noemi
Bonjour noemi,g strictement croissante donc monotone sur intervalle (1;4)
J'applique le TVI , l'équation g(x)=10 admet 1 solution car f(1) <10< f(4) donc -1<10<62.75 .
-
C'est correct, mais attention à la rigueur mathématiques
Ecriture d'un n intervalle [1 ; 4]
f(1) < 10 < f(4) car -1 < 10 < 62,75
-
mtschoon dernière édition par mtschoon

Tant qu'on est dans la rigueur, ce serait bien de préciser que f est continue et strictement monotone (cas de la bijection) , donc que l'équation g(x)=10 admet une solution unique
Un schéma pour éclairer
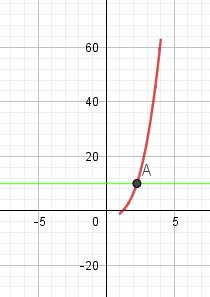
La solution unique de g(x)=10 est l'abscisse de A, intersection de la courbe représentative ( en rouge) et de la droite (en vert) d'équation y=10
Sur un schéma assez précis , on peut lire xA≈2.3x_A \approx 2.3xA≈2.3
-
Mmathiques dernière édition par mtschoon
Daccord merci de l'aide je vous montre la suite de l'exercice c'est un algorithme.
- L’algorithme ci-dessous permet d’obtenir un encadrement d’amplitude inférieure ou égale à
10^−1 de la solution α de l’équation g(x)=10 par la méthode de dichotomie.
Traitement : a prend la valeur 1
b prend la valeur 4
Tant que b−a>0,1 Faire
m prend la valeur a+b/2
y prend la valeur f(m)
Si y<10 Alors
a prend la valeur m
Sinon b prend la valeur m
Fin Si
Fin Tant que
Sortie : Afficher a et b
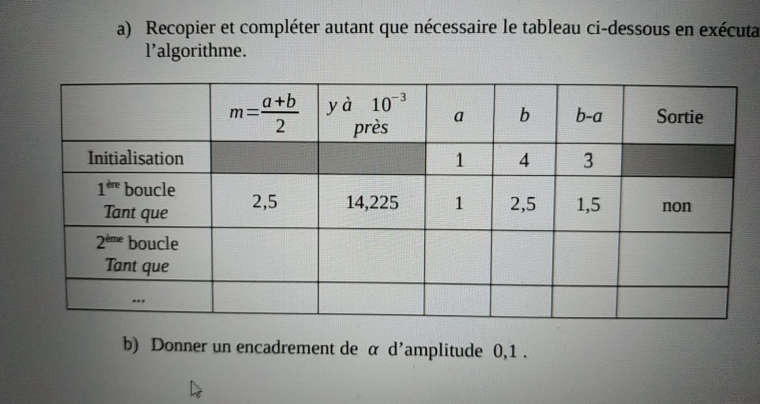
a) Recopier et compléter autant que nécessaire le tableau ci-dessous en exécutant
l’algorithme.
b) Donner un encadrement de α d’amplitude 0,1 .ps: un tableau va etre envoyé apres il se situe entre la question a et b .
- L’algorithme ci-dessous permet d’obtenir un encadrement d’amplitude inférieure ou égale à
-
?Un Ancien Utilisateur dernière édition par
-
mathiques,
Indique tes calculs
2ème boucle m = (1+2,5)/2 = .....
y = f(m) = ....
Test y est-il < 10 ?
a = ....
b = ....
b - a = .....et ainsi de suite
...
-
mtschoon dernière édition par mtschoon

As-tu compris le principe ?
J'en doute un peu vu que tu ne donnes pas les résultats du second tour de la boucle "tant que"comme te le demande Noemi.Si ça peut t'aider (?), je t'ai mis un lien pour une explication qui me semble claire.
Les notations a, b, m sont les mêmes que celles de ton énoncé.
La valeur appelée λ\lambdaλ dans le lien, vaut 10, donc dans ton exercice : λ=10\lambda=10λ=10
Pour la précision voulue, p=1p=1p=1 vu qu'ici la précision est de 0.1=10−10.1=10^{-1}0.1=10−1 .Faire le tableau de variation utile à chaque étape permet, peut-être, de mieux comprendre.
-
Mmathiques dernière édition par
Je pense avoir comprit l'algorithme ce termine au bout de la troisième boucle. car b=1.75 et a=1.75 donc 1.75-1.75=0 donc fin du programme.
-
Indique tes calculs,
as-tu tenu compte de l'indication si y <10 alors a = m ?
-
Mmathiques dernière édition par
@noemi oui j'en ai tenu compte c'est meme pour cela que l'algorithme ce fini.
-
Je n'ai pas dans mon tableau un a et un b égal à 1,75.
-
Mmathiques dernière édition par
ah mince
-
Mmathiques dernière édition par
Lors de la 3 boucle vu que y<10 alors a prend la valeur m qui était 1.75 , lors de la deuxième boucle b était égal a 1.75 donc 1.75-1.75=0
-
C'est lors de la deuxième boucle que y est < 10 donc a = 1,75 et b ne varie pas donc reste à 2,5.
Propose les résultats pour les boucles que tu as trouvées
Boucle 2 : m = 1,75 ; y = 3,788 ; a = 1,75 ; b = 2,5 ; b-a = 0,75 ; Sortie : non
Boucle 3 : ....
-
Mmathiques dernière édition par
@noemi Excuse moi je me suis trompé sur ma relecture...
-
Mmathiques dernière édition par
Boucle 3 : m= 2.125 y= 8.125 a=2.125 b=2.5 b-a=0.375 sortie: non
-
C'est correct.
-
Mmathiques dernière édition par
@noemi Bonjour,
J'ai trouvé que cela ce fini a la 5 boucle avec m=2.21875 y=9.472 a=2.21875 b=2.3125 b-a=0.09375 sortie : oui .
Pour la question B je trouve l'encadrement comprit entre 2.2 et 2.3 .
-
C'est correct.
-
Mmathiques dernière édition par
@noemi D'accord merci mais je n'arrive pas a faire le lien entre la réponse de l'algorithme et de la petite b ?
-
Tu as répondu à la question b) vu que tu as donné l'encadrement
2,2 < α\alphaα< 2,3
-
Mmathiques dernière édition par
@noemi mais normalement je devrait trouver le même résultat?
-
Avec quel résultat fais tu la comparaison ?
-
?Un Ancien Utilisateur dernière édition par
Avec le résultat a et b obtenu dans la boucle 5 ?
a= 2.21875 b = 2.3125
-
?Un Ancien Utilisateur dernière édition par
( Je travaille sur cet exercice avec @mathiques )
-
@chrosmiq75,
Il est demandé un résultat d'amplitude 0,1
Tu peux écrire 2,21 < α\alphaα < 2,31
-
Mmathiques dernière édition par
@noemi Dans notre algorithme a et b corresponde aux résultats trouvé pour l'encadrement de la question b?
-
Oui tous les intervalles [a ; b] contiennent la solution à l'équation f(x)=10f(x)=10f(x)=10,
A chaque étape, l'amplitude de l'intervalle diminue.
-
?Un Ancien Utilisateur dernière édition par
ET comment formuler la reponse sur ma copie?
-
Un encadrement α\alphaα d'amplitude 0,1 est 2,2 < α\alphaα < 2,3.
-
?Un Ancien Utilisateur dernière édition par Un Ancien Utilisateur
Ahh d'accord, donc vu que dans la boucle 5 on a trouvé 2.21875 et 2.3125 α\alphaα est compris enctre 2.2 et 2.3?
-
@chrosmiq75 ,
α\alphaα est compris entre 2,21875 et 2,3125 car b - a < 0,1
si on arrondi au dixième cela donne entre 2,2 et 2,3.