Exercice sur Probabilités 3ème
-
Ladi Loma dernière édition par
Bonsoir à tous
J'aurais besoin d'aide pour cette exercice
Merci de m'aiderMon exercise :
On tire au hasard un jeton dans la boite A et on note son numéro.
Ensuite on tire au hasard un jeton dans la boite B et on note son numéro. On a ainsi formé un nombre à deux chiffres.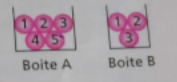
1- Peut -on obtenir le nombre 41? le nombre 34?
2- Construire un arbre pondéré à deux étapes pour représenter cette expérience.
3- Quelle est la probabilité que le nombre à deux chiffres obtenu soit:
a) 12?
b) un multiple de 2?
c) un multiple de4?
d) un nombre premier?
-
Bonjour Ladi-Loma ,
Indique tes éléments de réponse et la question qui te pose problème
1- Il suffit de vérifier :
si la boite A contient le chiffre des dizaines et la boite B celui des unités2- Construis l'arbre, première partie les éléments de la boite A, deuxième partie les éléments de la boite B
3- Pour le calcul des probabilités, calcule d'abord le total des nombres possibles
puis tu détermines pour chaque cas le nombre de réponse possible.
Tu calcules ensuite la probabilité correspondante.
-
mtschoon dernière édition par

Bonjour Ladi Loma et Noemi,
Piste pour t'éclairer sur le début si besoin
Question 1.
4 est dans la boite A et 1 est dans la boite B, donc on peut obtenir 41
3 est dans la boite A et 4 n'est dans la boite B, donc on ne peut pas obtenir 34Essaie de poursuivre.
-
Je t'ai indiqué des pistes, propose tes éléments de réponse.
Complète les ..........
1- On peut obtenir le nombre 41 car le 4 est dans la boite A et le 1 dans la boite B
On ne peut pas obtenir le nombre 34 car .......Bon mtschoon a donné la réponse.
2- Essaie de construire l'arbre
-
Ladi Loma dernière édition par
@mtschoon merci bcp

-
mtschoon dernière édition par mtschoon

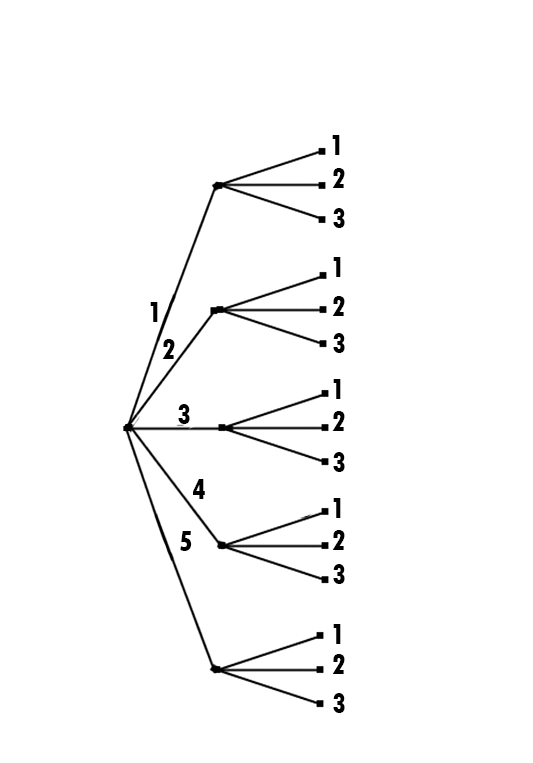
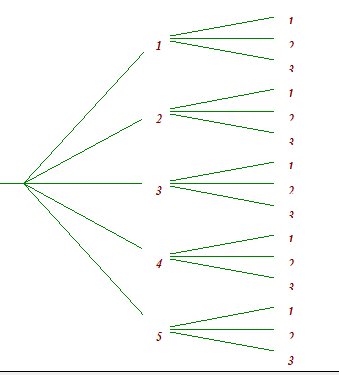
Je te donne un arbre, mais tu as dû voir le principe en cours , je suppose.
Si tu ne le comprends pas, demande, car recopier sans comprendre ne sert à rien...
L'idéal est que tu le fasses seule.
-
Ladi Loma dernière édition par
@mtschoon https://ibb.co/mhZByL c est juste?
-
mtschoon dernière édition par

Désolée mais de chez moi, je ne peut pas ouvrir l'image...
-
Ladi Loma dernière édition par
-
mtschoon dernière édition par

Cette fois, c'est bon et c'est exact.
Tu n'as plus qu'à utiliser l'arbre pour faire les calculs de la question 3.
Donne nous tes réponses si tu as besoin d'une vérification.
-
Ladi Loma dernière édition par
@mtschoon merci bcp
-
Ladi Loma dernière édition par Ladi Loma
@mtschoon @Noemi pour la question 3 c'est juste?
On utilise l'arbre construit précédemment
On a: p (1 ou 2) = p (1) + p(2) = 3/15 + 3/15 = 6/15 = 2/5
La probabilité que le nombre à deux chiffres obtenu: a) 12 est égale à 2/5
-
Ce qui est demandé, c'est la probabilité d'obtenir le nombre 12 et non 1 ou 2
Tu as obtenu avec l'arbre 15 résultats possibles, combien y a t-il de fois le nombre 12 ?
Tu en déduis la probabilité p(12) = ....
-
Ladi Loma dernière édition par Ladi Loma
@noemi @mtschoon c'est ça la question

3- Quelle est la probabilité que le nombre à deux chiffres obtenu soit:
a) 12?
b) un multiple de 2?
c) un multiple de4?
d) un nombre premier?
-
a) P(12) = la probabilité d'avoir le 1 en premier suivi du 2 en second,
Comme une seule possibilité cela donne P(12) = 1/15b) En utilisant l'arbre, indique les nombres obtenus qui sont multiples de 2 :
......
-
mtschoon dernière édition par mtschoon

J'espère que tu as compris l'usage de l'arbre(c'est le but de l'exercice)
Si tu suis tous les chemins (à partir du point de gauche), tu obtiens tous les nombres considérés :
11
12
13
21
22
...
...
53Comme te l'a indiqué Noemi, il y a 15 nombres (5×3=155 \times 3=155×3=15)
Parmi ces 15 nombres , un seul vaut 12 d'où la probabilité 115\frac{1}{15}151Pour la question b)
Parmi ces 15 nombres, tu cherches ceux qui sont multiples de 2 :
il y a 12, 22, ... tu continues de les énumérer
Tu dois en trouver 5
La probabilité sera donc 515=13\frac{5}{15}=\frac{1}{3}155=31La démarche est la même pour les questions c) et d)
Reposte si tu as besoin pour c) et d).
-
Ladi Loma dernière édition par Ladi Loma
@mtschoon @Noemi pour la question 3 c'est juste?
3- On utilise l'arbre construit précédemment.
a)
Parmi ces 15 nombres de possibilités , un seul vaut 12
D'où: p(12) = 1/15
la probabilité que le nombre à deux chiffres obtenu 12 est donc 1/15
b)
Parmi ces 15 nombres de possibilités, un multiple de 2 = (12,22,32,42,52)
D'où: p (un multiple de 2) = 5/15 = 1/3
la probabilité que le nombre à deux chiffres obtenu un multiple de 2 est donc 5/15
c'est à dire 1/3c)
Parmi ces 15 nombres de possibilités, un multiple de 4 = (12,32,52)
D'où: p (un multiple de 4) = 3/15 = 1/5
la probabilité que le nombre à deux chiffres obtenu un multiple de 4 est donc 3/15
c'est à dire 1/5d)
Parmi ces 15 nombres de possibilités, un nombre premier = (11,13,21,23,31,33,41,43,51,53)
D'où: p (un nombre premier) = 10/15 = 2/3
la probabilité que le nombre à deux chiffres obtenu un nombre premier est donc 10/15 c'est à dire 2/3
-
mtschoon dernière édition par

Je regarde tes réponses
a) c'est bon
b) c'est bon
c) c'est bon
d) Il y a 3 nombres de trop
21, 33, 51 ne sont pas premiers car :
21=3×721=3 \times 721=3×7
33=3×1133=3\times 1133=3×11
51=3×1751=3\times 1751=3×17
-
Ladi Loma dernière édition par
@mtschoon d)
Parmi ces 15 nombres de possibilités, un nombre premier = (11,13,23,31,41,43,53)
D'où: p (un nombre premier) = 7/15
la probabilité que le nombre à deux chiffres obtenu un nombre premier est donc 7/15
-
mtschoon dernière édition par

C'est tout bon !
-
Ladi Loma dernière édition par
@mtschoon merci bcp
-
mtschoon dernière édition par

De rien Ladi Loma !
A+
-
TTariacity dernière édition par
@Ladi-Loma bonjour,
Qui.peut m'éclairer svp :
Pk dériver 1 et 2 et 3 de chaque chiffre ? Je n'ai pas compris le.motif .
On ne.pioche que 2 fois : une.de chaque boiteMerci d'avance
-
@Tariacity Bonjour,
L'arbre indique toutes les possibilités.
Si on choisit 1 dans la boite A, on peut y associer, 1, 2 ou 3 de la boite B
Si on choisit 2 dans la boite A, ....
et ainsi de suite.