différence entre la dérivabilité et la continuité
-
SsaraSBH dernière édition par
Bonjour ,
c'est quoi la différence entre la dérivabilité et la continuité ,et comment les justifier chacune en un réel. aidez moi svp
-
mtschoon dernière édition par

saraSBH, bonsoir
J'ignore si tu parles de continuité et dérivabilité pour une valeur a de la variable ou sur un intervalle
Pour faire simple,
f continue en a : limx→af(x)=f(a)\displaystyle \lim_{x\to a}f(x)=f(a)x→alimf(x)=f(a)
f dérivable en a : limx→af(x)−f(a)x−a=f′(a)\displaystyle \lim_{x\to a}\frac{f(x)-f(a)}{x-a}=f'(a)x→alimx−af(x)−f(a)=f′(a)
Par théorème, si f est dérivable en a, elle est continue en a.
La réciproque n'est pas vraie.Donne des exemples précis, si tu as besoin.
-
SsaraSBH dernière édition par saraSBH
bonsoir, @mtschoon
merci beaucoup ! mais comment faire pour les justifier sur un intervalle ?
je peut utiliser lim f(x)−f(a)/x−a = f'(a) pour justifier la continuité ?
x→a
-
mtschoon dernière édition par

Pour justifier les définitions sur un intervalle I, les définitions doivent s'appliquer pour toute valeur a de l'intervalle I.
Pour justifier la continuité, tu utilises la définition de continuité donnée.
Donne un énoncé précis pour clarifier tes questions.
-
mtschoon dernière édition par mtschoon

Je te donne un exemple, mais j'ignore s'il est adapté à ton cours.
Soit f(x)=∣x2−1∣f(x)=|x^2-1|f(x)=∣x2−1∣
Explicitation des deux expressions sans symboles de valeurs absolues
1er cas : x∈]∞,−1]∪[1,+∞[x\in ]\infty,-1]\cup [1,+\infty[x∈]∞,−1]∪[1,+∞[
x2−1≥0x^2-1 \ge 0x2−1≥0 donc f(x)=x2−1f(x)=x^2-1f(x)=x2−12ème cas : x∈−1,1]x\in-1,1]x∈−1,1]
x2−1≤0x^2-1 \le 0x2−1≤0 donc f(x)=−(x2−1)=−x2+1f(x)=-(x^2-1)=-x^2+1f(x)=−(x2−1)=−x2+1Représentation graphique :
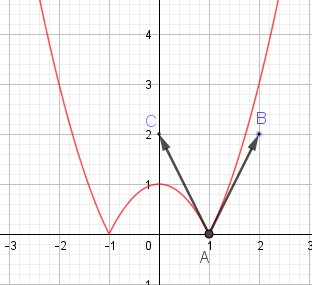
Etude de la continuité en x= 1
f(1)=0f(1)=0f(1)=0
limx→1f(x)=limx→1∣x2−1∣=∣1−1∣=0=f(1)\displaystyle \lim_{x\to 1}f(x)=\lim_{x\to 1}|x^2-1|=|1-1|=0=f(1)x→1limf(x)=x→1lim∣x2−1∣=∣1−1∣=0=f(1)
D'après la définition, f est continue en x=1
Graphiquement , la courbe en rouge est représentée par un trait continue au voisinage du point A(1,0)Etude de la dérivabilité en x=1
dérivabilité à droite
x tend vers 1 par valeurs supérieures à 1 : on note "x tend vers 1+"
limx→1+f(x)−f(1)x−1=limx→1+x2−1−0x−1=limx→1+x2−1x−1=limx→1+x2−1x−1\displaystyle \lim_{x\to 1^+}\frac{f(x)-f(1)}{x-1}=\lim_{x\to 1^+}\frac{x^2-1-0}{x-1}=\lim_{x\to 1^+}\frac{x^2-1}{x-1}=\lim_{x\to 1^+}\frac{x^2-1}{x-1}x→1+limx−1f(x)−f(1)=x→1+limx−1x2−1−0=x→1+limx−1x2−1=x→1+limx−1x2−1Avec l'identité remarquable
limx→1+f(x)−f(1)x−1=limx→1+(x+1)(x−1)x+1=limx→1+(x+1)=2\displaystyle \lim_{x\to 1^+}\frac{f(x)-f(1)}{x-1}= \lim_{x\to 1^+}\frac{(x+1)(x-1)}{x+1}= \lim_{x\to 1^+}(x+1)=2x→1+limx−1f(x)−f(1)=x→1+limx+1(x+1)(x−1)=x→1+lim(x+1)=22 est le nombre dérivé à droite (c'est le coefficient directeur de le demi-tangente à droite,à la courbe au point A (vecteur directeur AB→\overrightarrow{AB}AB)
dérivabilité à gauche
x tend vers 1 par valeurs inférieures à 1 : on note "x tend vers 1-"
Même principe en prenant f(x)=−x2+1f(x)=-x^2+1f(x)=−x2+1
On trouve
limx→1−f(x)−f(1)x−1=−2\displaystyle \lim_{x\to 1^-}\frac{f(x)-f(1)}{x-1}=-2x→1−limx−1f(x)−f(1)=−2
-2 est le nombre dérivé à gauche (c'est le coefficient directeur de le demi-tangente à gauche,à la courbe au point A (vecteur directeur AC→\overrightarrow{AC}AC)Vu que 2≠−22\ne-22=−2 f n'est pas dérivable en x=1
(si f était dérivable en x=1, il y aurait UN (seul) nombre dérivé qui se noterait f'(1) et la courbe aurait UNE tangente au point A de coefficient directeur f'(1))