Problème de factorisation pour étude de fonction
-
GGabin Cellerier dernière édition par mtschoon
Bonjour, j'ai quelques questions en ce qui concerne un dm de math que je n'arrive pas à résoudre, vous pourriez m'aider svp?
Voici les questions:
Soit f la fonction déinie par
f(x)=x2−4x−1x−2f(x)=\frac{x^2-4x-1}{x-2}f(x)=x−2x2−4x−1
et Cf sa courbe dans un repère.
(a) Démontrer que ∀x ∈ R,
x2−4x−1=(x−2)2−5x^2-4x-1=(x-2)^2-5x2−4x−1=(x−2)2−5
(b) En déduire une factorisation de x
x2−4x−1x^2-4x-1x2−4x−1
(c) Déterminer les coordonnées des points d'intersection de Cf avec les axes de coordonnées.(Formules re-écrites en Latex)
-
mtschoon dernière édition par mtschoon

Gabin Cellerier , bonjour,
Piste,
a) x2−4x−1=x2−4x+4−1−4=x2−4x+4−5=(x−2)2−5x^2-4x-1=x^2-4x+4-1-4=x^2-4x+4-5=(x-2)^2-5x2−4x−1=x2−4x+4−1−4=x2−4x+4−5=(x−2)2−5
Si tu préfères, mais c'est moins bien car tu pars de la conclusion à démontrer, tu développes (x−2)2−5(x-2)^2-5(x−2)2−5 et tu trouves le membre de gauche de l'égalité
b)(x−2)2−5(x-2)^2-5(x−2)2−5 est de la forme a²-b² avec a=x−2a=x-2a=x−2 et b=5b=\sqrt 5b=5
Tu factorises donc avec l'identité a2−b2=(a−b)(a+b)a^2-b^2=(a-b)(a+b)a2−b2=(a−b)(a+b)
-
mtschoon dernière édition par

Piste pour la c)
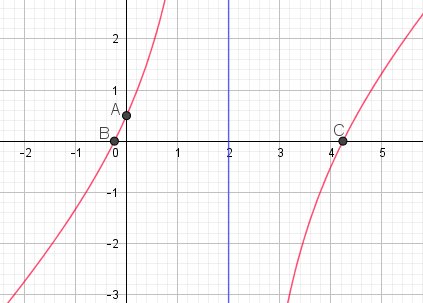
Df=R-{2}
x=2 est l'équation de l'asymptote "verticale" (en bleu)Intersection avec l'axe des ordonnées :A(0,f(0))A(0,f(0))A(0,f(0)) calculer f(0)f(0)f(0)
Intersection avec l'axe des abscisses : B(x1,0B(x_1, 0B(x1,0) et C(x2,0)C(x_2,0)C(x2,0)
x1x_1x1 et x2x_2x2 sont les solutions de l'équation f(x)=0, c'est à dire de x2−4x−1=0x^2-4x-1=0x2−4x−1=0, qui se trouvent facilement avec la factorisation faite au b)