les racines carrées d'un nombre complexe
-
SsaraSBH dernière édition par mtschoon
bonsoir ,
j'arrive pas à déterminer la racine carré de -1-i et -1+i
aidez moi svp.
-
mtschoon dernière édition par mtschoon

saraSBH , bonsoir,
Tout nombre complexe non nul a deux racines carrées distinctes complexes
Si veux traiter l'exercice avec les complexes mis sous forme algébrique, je te mets un lien pour le principe :https://homeomath2.imingo.net/complex9.htm
Piste pour -1-i
Tu cherches x et y réels tels que (x+iy)2=−1−i(x+iy)^2=-1-i(x+iy)2=−1−i
En développant x2−y2+2xyi=−1−ix^2-y^2+2xyi=-1-ix2−y2+2xyi=−1−i
En identifiant les parties rélles entre elles : x2−y2=−1x^2-y^2=-1x2−y2=−1
En identifiant les parties imaginaires entre elles : 2xy=−12xy=-12xy=−1Tu as donc à résoudre le système :
x2−y2=−1x^2-y^2=-1x2−y2=−1
2xy=−12xy=-12xy=−1
(désolée pour l'absence d'accolade, mais la latex actuel ne le permet pas...)Si tu en as l'habitude (regarde ton cours) , tu peux t'aider de l'égalité des modules
x2+y2=(−1)2+(−1)2x^2+y^2=\sqrt{(-1)^2+(-1)^2}x2+y2=(−1)2+(−1)2 <=> x2+y2=2x^2+y^2=\sqrt 2x2+y2=2Essaie de faire les calculs et reposte si besoin.
-
mtschoon dernière édition par mtschoon

Je viens de faire les calculs pour -1-i.
x2−y2=−1x^2-y^2=-1x2−y2=−1
x2+y2=2x^2+y^2=\sqrt 2x2+y2=2On obtient , sauf erreur, x2=2−12x^2=\frac{\sqrt 2-1}{2}x2=22−1 et y2=2+12y^2=\frac{\sqrt 2+1}{2}y2=22+1
D'où
x=±2−12x=\pm\sqrt{\frac{\sqrt 2-1}{2}} x=±22−1 et y=±2+12y=\pm\sqrt{\frac{\sqrt 2+1}{2}} y=±22+1Vu que 2xy=−12xy=-12xy=−1 , x et y sont de signes contraires
Conclusion:
x=+2−12x=+\sqrt{\frac{\sqrt 2-1}{2}} x=+22−1 et y=−2+12y=-\sqrt{\frac{\sqrt 2+1}{2}} y=−22+1
ou bien
x=−2−12x=-\sqrt{\frac{\sqrt 2-1}{2}} x=−22−1 et y=+2+12y=+\sqrt{\frac{\sqrt 2+1}{2}} y=+22+1
Les racines carrées complexes de -1-i sont:
$\fbox{+\sqrt{\frac{\sqrt 2-1}{2}}-i\sqrt{\frac{\sqrt 2+1}{2}}} $
et
$\fbox{-\sqrt{\frac{\sqrt 2-1}{2}}+i\sqrt{\frac{\sqrt 2+1}{2}}} $*Remarque :
Vu que l'argument de -1-i est remarquable, tu peux aussi traiter l'exercice avec les complexes mis sous forme exponentielle (ou trigonométrique)
-
mtschoon dernière édition par mtschoon

Si tu veux traiter l'exercice avec la forme exponentielle,
Après calcul :
−1−i=2e−3iπ4-1-i=\sqrt 2e^{-\frac{3i\pi}{4}}−1−i=2e−43iπ(reiθ)2=2e−3iπ4(re^{i\theta})^2=\sqrt 2e^{-\frac{3i\pi}{4}}(reiθ)2=2e−43iπ
r2e2iθ=2e−3iπ4r^2e^{2i\theta}=\sqrt 2e^{-\frac{3i\pi}{4}}r2e2iθ=2e−43iπ
d'où
r2=2r^2=\sqrt 2r2=2 <=>r=2r=\sqrt{\sqrt 2}r=2 <=> r=214r=2^{\frac{1}{4}}r=241
Pour k∈Zk\in Zk∈Z
2θ=−3π4+2kπ2\theta=-\frac{3\pi}{4}+2k\pi2θ=−43π+2kπ <=> θ=−3π8+kπ\theta=-\frac{3\pi}{8}+k\piθ=−83π+kπLes deux racines carrées de -1-i sont les nombres :
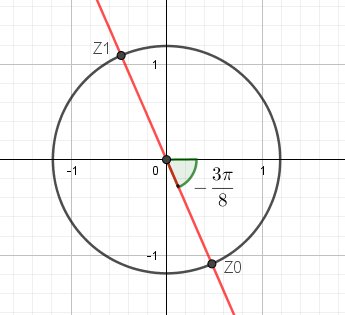
$\fbox{z=2^\frac{1}{4}e^{i(\frac{-3\pi}{8}+k\pi)}}$
-
mtschoon dernière édition par mtschoon

Complémént : Représentation graphique des deux racines carrées de -1-i , dans le plan complexe