Exercice à preparer 3e maths
-
Eemmxxx dernière édition par
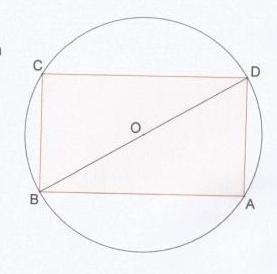
Voici ma figure :
La question est :
On considère le rectangle ci-contre inscrit dans un cercle de diamètre 4 cm.
On souhaite déterminer la longueur AB au mm près qui permettra d'obtenir l'aire maximale du rectangle ABCD.
Merci de bien vouloir m'aider !
-
mtschoon dernière édition par mtschoon

emmxxx bonsoir,
C'est très bien d'avoir joint la figure, Merci !
Une piste algébrique possible pour "préparer ton exercice"
Vu que tu cherches la longueur AB, tu peux poser AB=x
Nécessairement 0≤x≤40 \le x \le 40≤x≤4 (car diagonale du rectangle=4cm)Avec le théorème de Pythagore:
AB²+AD²=BD² c'est à dire x²+AD²=16 <=> AD²=16-x²
AD=16−x2AD=\sqrt{16-x^2}AD=16−x2L'aire d'un rectangle est donc f(x)=x16−x2f(x)=x\sqrt{16-x^2}f(x)=x16−x2
Avec une méthode dont tu as l'habitude j'espère (calculette graphique avec la fonction table ou Tableur) il te reste à donner la valeur de x (comprise entre 0 et 4) , à 1mm près (c'est à dire à 0.1 près vu que l'unité utilisée est le cm), pour laquelle f(x) est maximale.
Reposte si besoin.
-
Bonsoir emmxxx et mtschoon,
C'est un exercice niveau 3ème, donc je propose une solution plus simple.
Le rectangle ABCD est constitué de deux triangles identiques ABD et CBD, donc son aire est maximale si l'aire d'un triangle est maximale.
L'aire du triangle ABD = BD x h / 2 si h est la hauteur issue du point A.
L'aire du rectangle est donc BD x h
vu que BD = 4 cm, l'aire est maximale si h est maximale et la plus grande hauteur que l'on peut tracer correspond au rayon, soit 2 cm.
Donc le triangle BOA est rectangle isocèle en O.
Je te laisse calculer BA sachant que OB = OA = 2.Propose ta réponse pour le calcul de BA si tu souhaites une correction.
-
mtschoon dernière édition par mtschoon

Bonjour emmxxx et Noemi,
@emmxxx
Tu as ainsi deux possibilités pour traiter ton exercice.Ma proposition est tournée vers une démonstration type plutôt lycée.
La proposition de Noemi est tournée vers une observation type collège.Utilise la méthode qui est la plus adaptée à ton cours actuel et qui te convient le mieux.
Eventuellement, si tu maîtrises les deux méthodes, tu fais les deux et tu vérifies que tu trouves le même résultat.
-
mtschoon dernière édition par

Pour pouvoir vérifier :
Sauf erreur : x≈2.8x\approx 2.8x≈2.8
-
Eemmxxx dernière édition par
Bonsoir mtschoon et noemi,
Excusez moi de ne pas vous avoir répondu plus tôt,
Déjà merci car ça ma vraiment aider
J'ai pas trop trop compris mais je vais le revoir ce week-end ou bien dans la semaine prochaine.
Si ça ne vous dérange pas, je vous poserais peut-être des questions par la suite.
Un grande merci à vous deux.
-
Bonsoir emmxxx,
N'hésite pas à nous poser les questions ou toutes demandes d'explication.
-
Eemmxxx dernière édition par
Bonjour Noemi,
BA=4 cm car c'est un triangle isocèle donc les deux côté sont identiques (de même longueurs).
Je ne comprends pourquoi vous avez marqué BOA alors qu'il n'y a pas de rectangle BOA.
Merci de bien vouloir m'expliquer.
-
Bonjour emmxxx,
OA est la hauteur du triangle ABD, donc (OA) est perpendiculaire à (BD)
comme [OA] = [OB], le triangle OAB est donc rectangle isocèle en O.
-
Eemmxxx dernière édition par
D'accord merci !

Vous m'avez demander de dire BA=?
Donc, BA=4cm
C'est bien cela ?
-
Non,
Pour calculer BABABA tu appliques la propriété de Pythagore.
BA2=OA2+OB2BA^2=OA^2+OB^2BA2=OA2+OB2
-
Eemmxxx dernière édition par
Haaa d'accord !
donc :
BA²=OA²+OB²
BA²= 2²+2²
BA²= 4 + 4
BA²= 8
BA= √8
Est-ce cela ?
merci beaucoup
-
Oui c'est correct,
Tu peux écrire 8=22\sqrt8 = 2\sqrt28=22
puis indiquer la longueur de AB au mm près.
-
Eemmxxx dernière édition par
Donc, AB² = 28 mm
es ce cela ?
-
C'est juste.
-
Eemmxxx dernière édition par
D'accord. Merci beaucoupppp

Après que dois - je chercher ?
-
Eemmxxx dernière édition par
La prof nous a dit de le faire en fonction de x donc je ne sais pas si nous avons bien rédiger
-
Bonjour emmxxx,
Essaie de faire la méthode proposée par mtschoon.
Indique tes questions si tu ne comprends pas.
-
Eemmxxx dernière édition par
D'accord je vais essayer
-
mtschoon dernière édition par mtschoon

Bonjour emmxxx et bonjour Noemi,
@emmxxx
Si ton professeur veut la solution avec l'inconnue "x" , c'est la méthode algébrique que je t'ai proposée qui semble être celle qu'il te faut.
(tu aurais dû l'indiquer dès le début avec l'énoncé...)
Je n'ai peut-être pas trop détaillé le principe, alors demande ce que tu ne comprends pas.
-
C'est le théorème de Pythagore
BD2=AB2+AD2BD^2 = AB^2 + AD^2BD2=AB2+AD2
si on pose AB=xAB = xAB=x la relation devient
42=x2+AD24^2 = x^2 + AD^242=x2+AD2
d'ou AD=.....AD = .....AD=.....
-
mtschoon dernière édition par mtschoon

@mtschoon a dit dans Exercice à preparer 3e maths :
AB²+AD²=BD² c'est à dire x²+AD²=16 <=> AD²=16-x²
(Le diamètre du cercle est BD=4 donc BD²=16)
-
Eemmxxx dernière édition par
Haa d'accord merci

-
mtschoon dernière édition par

De rien emmxxx.
Reposte si tu as un problème pour terminer.
-
Eemmxxx dernière édition par
@mtschoon
Voila ce que j'ai fais, dites moi si cela va pour le moment :
Je sais que le cercle est de diamètre 4 cm.
Je cherche la longueur de AB donc on peut dire que AB= x.
x sera obligatoirement compris entre 0 et 4 car la diagonale du rectangle est égale à 4 cm.
Pour trouver AB, je vais utiliser le Théorème de Pythagore,
Je sais que BD = 4 cm et AB = x.
D'après le Théorème de Pythagore,
AB²+AD²=BD²
x²+ AD² = 4²
AD² = 16 – x²
AD = 16 – x²
Donc, l'aire du rectangle est donc f(x) = 16 – x²

-
Eemmxxx dernière édition par
Non, je me suis trompée.
AD = √16 - x²
Donc, l'aire du rectangle est f(x) = x√16 - x²
Est-ce cela ??

-
mtschoon dernière édition par mtschoon

Oui,ta dernière réponse est bonne.
l'aire du rectangle est f(x)=x×16−x2f(x)=x\times \sqrt{16-x^2}f(x)=x×16−x2
On écrit usuellement f(x)=x16−x2f(x)=x\sqrt{16-x^2}f(x)=x16−x2
-
Eemmxxx dernière édition par
Merciii
Donc j'ai maintenant l'aire = f(x) = x√16 - x²
Mais, il me manque la longueur de AB au mm près.
Je ne vois pas comment la trouver.
Pouvez-vous m'aider ?

-
Bonjour emmxxx,
Que connais tu sur les fonctions ?
-
Eemmxxx dernière édition par
Je l'ai est vu oui.
Nous avons fais les images ainsi que les antécédents.
Je ne sais pas trop comment vous l'expliquez
-
Tu as vu les fonctions avec racine carrée ?
Tu utilises ta calculatrice pour calculer les images ? un maximum ?
-
mtschoon dernière édition par mtschoon

Bonjour Noemi,
Je crains que emmxxx ne connaisse pas grand'chose de ces fonctions ...
En consultant un manuel actuel de Seconde, je constate que les représentations graphiques, calculettes, tableurs, sont très à la mode.
Comme je l'avais indiqué dans mon premier message, je pense que c'est vers un de ces outils qu'il doit se tourner.
-
Bonjour mtschoon, emmxxx
Tu indiques la classe de Seconde, mais le post est sur la classe 3ème.
Emmxxx est-il en seconde ?
-
Eemmxxx dernière édition par
@mtschoon et @Noemi
Oui j'utilise la calculatrice pour calculer les images et faire des tableaux si besoin.
-
Eemmxxx dernière édition par
Là nous avons trouver l'aire du rectangle mais pas l'aire maximale c'est bien ça ?
Là je dois trouver AB au mm près et après l'aire maximale de ABCD. C'est bien cela ??

-
mtschoon dernière édition par

Exact Noemi, emmxxx poste en 3ème.
En 3ème, emmxxx doit savoir encore moins de choses sur les fonctions que s'il etait en Seconde !
(Il faudra qu'il attende d'être en Première pour savoir étudier ce type de fonction...)
-
Eemmxxx dernière édition par
@mtschoon Est-ce bien cela ? (par rapport à mon dernier message )

-
mtschoon dernière édition par

f(x) est l'aire du rectangle, en fonction de x
Tu dois trouver (avec une méthode que tu connais) la valeur de x pour laquelle cette fonction a son maximum (sur l'intervalle (0,4])
-
Oui tu remplaces xxx par des valeurs variant de 0 à 4 avec un pas de 0,1 avec la calculatrice pour chercher la valeur de AB et l'aire maximale.
-
Eemmxxx dernière édition par
Haa d'accord je vais essayer mercii beaucoupp à vous deux !!!

-
mtschoon dernière édition par

Si tu ne fais pas d'erreur, tu dois trouver (pour le maximum), la valeur de x que je t'ai indiquée au début de cette (longue) discussion et que tu as trouvée avec l'autre méthode proposée par Noemi.
-
Eemmxxx dernière édition par
J'ai trouvé que x = 2,8etf(x)=7,998399842,8 et f(x) = 7,998399842,8etf(x)=7,99839984
Est-ce cela ?
@mtschoon & @Noemi
-
mtschoon dernière édition par

OUI ! c'est bon.
-
Oui c'est correct, tu peux arrondir l'aire.
-
Eemmxxx dernière édition par
Oui je viens de m'en apercevoir. Et bien nous avons trouver la même chose 2,8.
Donc, j'ai fais le tableau du début 0 et de la fin 4 avec un pas de 0,1 et juste je ne comprends ce que signifie f(x) dans le tableau = 7,99839984
( Je sais je ne comprends pas grand chose mais j'en profite pour vous posez des questions)
-
mtschoon dernière édition par mtschoon

Une remarque emmxxx,
La valeur exacte (que tu as trouvée avec la méthode "géométrique" est 8\sqrt 88
Si tu calcules f(8)f(\sqrt 8)f(8) , tu trouveras exactement 8
-
Nous te l'avons indiqué, f(x) est l'aire du rectangle.
-
Eemmxxx dernière édition par
AB = 2,8 cm et comme il le demande en mm AB = 28 mm.
Donc, l'aire maximale est 7,99839984
Est-ce bien cela ?
-
mtschoon dernière édition par mtschoon

Oui, la valeur approchée pour AB est 2.8cm c'est à dire 28 mm.
Comme Noemi te l'a déjà dit , tu peux arrondir l'aire maximale à 8 cm² (qui est, en fait, la valeur exacte).
-
Eemmxxx dernière édition par
Merciiii beaucoup à vous deuxxxx

-
mtschoon dernière édition par

De rien !

Revois tout cela pour être sur(e) d'avoir bien compris.
-
Eemmxxx dernière édition par
Oui je suis en train.
Merciiii
-
Eemmxxx dernière édition par
Je peux vous copie coller ce que j'ai marquer pour savoir si cela va ??

-
Eemmxxx dernière édition par
e sais que le cercle est de diamètre 4 cm.
Je cherche la longueur de AB donc on peut dire que AB= x.
x sera obligatoirement compris entre 0 et 4 car l'hypoténuse du rectangle DBA est égale à 4 cm.
Pour trouver AB, je vais utiliser le Théorème de Pythagore,
Je sais que BD = 4 cm et AB = x.
D'après le Théorème de Pythagore,
AB²+AD²=BD²
x²+ AD² = 4²
AD² = 16 – x²
AD = √16 – x²
L'aire d'un rectangle c'est longueur × largeur.
AB × AD = x × √16 – x²
Donc, l'aire du rectangle est donc f(x) = x √16 – x²Je fais un tableau en remplaçant x par des valeurs variant entre 0 et 4 car l'hypoténuse du rectangle DBA est égale à 4 cm. Cela me permettra de trouver la valeur de AB et l'aire maximale du rectangle ABCD.
( Le tableau sera ici )On observe que l'aire est la plus grande quand x = 2,8 mm. On converse 2,8 cm en mm, ce qui nous donne 28 mm.
Donc, AB ≈ 28 mm près.
Comme j'ai trouvé que la longueur de AB, je peux maintenant trouver l'aire maximale.
Dans le tableau si dessus, on observe que 2,8 = 7,9983 = √8.
√8 est la valeur exacte.
Donc, l'aire maximale du rectangle ABCD est 8 cm².
Est-ce bon ??

(Après je ne vous embette plus @mtschoon )
-
mtschoon dernière édition par mtschoon

Pas de soucis emmxxx.
Tu n'embêtes personne !Ton explication est correcte sauf pour une égalité où tu mélanges les valeurs de x avec celle de f(x)
Tu as écrit on observe que 2,8 = 7,9983 = √8
Il faut séparer la valeur de AB avec celle de ABCDMAXIMUM
Pour AB : 2.8≈82.8 \approx \sqrt 82.8≈8
Pour l'aire ABCD : f(2.8)≈f(8)f(2.8) \approx f(\sqrt 8 )f(2.8)≈f(8)
f(8)=8f(\sqrt 8)=8f(8)=8
-
Eemmxxx dernière édition par
Si je fais la formule en remplaçant x par 2,8 je trouve 8 ou √8 ??
-
Tu dois trouver 8.
-
Eemmxxx dernière édition par
-
Eemmxxx dernière édition par
On observe que l'aire est la plus grande quand x = 2,8 mm. On converse 2,8 cm en mm, ce qui nous donne 28 mm.
Donc, AB ≈ 28 mm près.
Comme j'ai trouvé que la longueur de AB, je peux maintenant trouver l'aire maximale.
Je sais que le cercle est de diamètre 4 cm.
Je cherche la longueur de AB donc on peut dire que AB= x.
x sera obligatoirement compris entre 0 et 4 car l'hypoténuse du rectangle DBA est égale à 4 cm.
Pour trouver AB, je vais utiliser le Théorème de Pythagore,
Je sais que BD = 4 cm et AB = x.
D'après le Théorème de Pythagore,
AB²+AD²=BD²
x²+ AD² = 4²
AD² = 16 – x²
AD = √16 – x²
L'aire d'un rectangle c'est longueur × largeur.
AB × AD = x × √16 – x²
Donc, l'aire du rectangle est donc f(x) = x √16 – x²Je fais un tableau en remplaçant x par des valeurs variant entre 0 et 4 car l'hypoténuse du rectangle DBA est égale à 4 cm. Cela me permettra de trouver la valeur de AB et l'aire maximale du rectangle ABCD.
( Tableau)
On observe que 2,8² = √8.
√8 est la valeur exacte.
On remplace x par √8. La formule est f(√8) = √8 × √16 – √8² ≈ 8.
Donc, l'aire maximale du rectangle ABCD est 8 cm².
Voila, normalement ça devrai être juste. Dites moi
@mtschoon & @Noemi
-
Eemmxxx dernière édition par
Pardon, √8 × √16 – √8² = 8.
(J'avais marqué que cela était ENVIRON égal à 8 )
-
mtschoon dernière édition par mtschoon

Tu demandes : pourquoi avez vous marquez que AB = √8 et pas 8 ?
Réponse :
AB=8AB=\sqrt 8AB=8
aire(ABCD)=8aire(ABCD)=8aire(ABCD)=8
Ne confonds pas les deux...Je regarde l'ensemble
Tu as écrit 2,8² = √8 : c'est faux 8≈2.8\sqrt 8\approx 2.88≈2.8Tu as écrit f(√8) = √8 × √16 – √8² = 8.
L'écriture n'est pas bonne.
f(8)=816−(8)2=816−8=88=8f(\sqrt 8)=\sqrt 8\sqrt{16-(\sqrt 8)^2}=\sqrt 8\sqrt{16-8}=\sqrt 8\sqrt 8=8f(8)=816−(8)2=816−8=88=8
-
Eemmxxx dernière édition par
Haa oui je viens de voir ! Mercii beaucoup @mtschoon !!

J'ai corriger cela et normalement tout est juste après !
-
Eemmxxx dernière édition par emmxxx
@mtschoon Entre le premier √8 et √16 ... Il y a bien un multiplier (×) ??
-
mtschoon dernière édition par

Oui.
Lorsqu'il y a deux nombres A et B, le produit A×BA\times BA×B peut s'écrire plus simplement ABABAB
-
Eemmxxx dernière édition par
D'accord mercii beacouppp !!

Et pour le tableau, je commence à écrire donc deux lignes avec x et l'autre avec f(x) = x × √16 - x² et je marque donc 0 et en bas 0 ainsi de suite mais au lieu de tout écrire ( car ça ne rentrera jamais sur ma feuille si j'écris tout le tableau et en plus le pas est de 0,1) je peux faire un case avec trois petits points dedans et ensuite reprends plus loin ??
Je ne sais pas si vous avec compris
-
mtschoon dernière édition par

Oui, j'ai compris, mais là, c'est à toi de voir la rédaction sur ta copie.
Les "petits points" me paraissent convenir, mais c'est à ton professeur de juger !
-
Eemmxxx dernière édition par
C'est elle qui nous à dit que l'on pouvais les faire. Je lui demanderai pour être sur !
Encore mercii @mtschoon !!
-
mtschoon dernière édition par mtschoon

Une réflexion finale sur le sujet.
Avec la méthode algébrique (avec l'inconnue x et la calculette ) tu ne peux avoir, pour AB, que la valeur approchée 2.8 cm (qui est demandée).
Si tu veux obtenir , pour AB ,bien qu'elle ne soit pas vraiment demandée, la valeur exacte 8\sqrt 88, en toute rigueur, il faudrait que tu rédiges, en complément, la méthode géométrique proposée par Noemi.
Evidemment, ça te complique la rédaction...c'est à toi de voir...
Je crois que l'on a fait maintenant le tour de la question.
Bon travail !

-
Eemmxxx dernière édition par
Je pense que je vais rester sur ce que j'ai fais. Car il demande une valeur au mm près et c'est bien ce que j'ai fais ! Et aussi parce que j'ai dit que AB devais obligatoirement être compris entre 0 et 4 car l’hypoténuse est égale à 4 cm. Si je laisse mon devoir comme cela, ça va je n'est pas d'erreurs ??
@mtschoon
-
mtschoon dernière édition par mtschoon

Je pense que tu ne fais pas d'erreurs ainsi .
(Le calcul de la valeur exacte de AB (8\sqrt 88) aurait été un supplément)En tout cas, tu as bien travaillé !

-
Eemmxxx dernière édition par
Mercii ! Mais c'est vous qui m'avez bien aider !!

-
mtschoon dernière édition par

C'est normal.
C'est le but du forum.
Bonnes vacances
-
Eemmxxx dernière édition par
Bonnes vacances

-
mtschoon dernière édition par

Merci

-
Eemmxxx dernière édition par
Bonjour, @mtschoon
J'ai posé cette question à la prof par rapport au tableau:
Est-ce que au lieu de marquer tout les nombres dans le tableau, on peut mettre trois points de suspension et continuer à un autre nombre ?
Mais je n'ai pas compris comment elle veut que je fasse le tableau:
Il faut choisir des valeurs intéressantes : un pas assez grand au départ, une valeur de fin bien étudiée : peut-on avoir un côté de 10 cm avec une diagonale de 4 cm ? Et après refaire un tableau avec un pas plus petit avec deux nouvelles valeurs de début et de fin bien choisies. Ainsi une dizaine de valeurs par tableau devraient suffire. Pas la peine d'avoir un tableau trop chargé.
Pouvez-vous me l'expliquez ?? Merci
-
Bonjour emmxxx,
Au début tu choisis un pas de 1, donc tu as un tableau avec 5 valeurs.
Tu en déduis que le nombre est compris entre 2 et 3.
Puis tu fais un tableau avec un pas de 0,1, de 2,1 à 2,9 soit 9 valeurs.
-
Eemmxxx dernière édition par
D'accord donc on a différents nombres genre pour 1 c'est compris entre 2 et 3 et pour 0,1 c'est compris entre deux autres nombres ?

Merci @Noemi
-
mtschoon dernière édition par mtschoon

Bonjour emmxxx et Noemi,
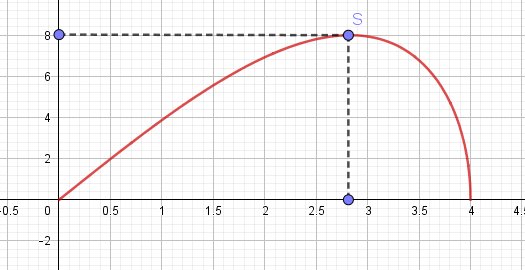
Avec les valeurs que tu as utilisées pour le(s) tableau(x), tu peux peut-être, pour illustration, si tu le trouves utile, faire la représentation graphique de la fonction f
Je te joins la courbe (faite avec geogebra)
-
Tu as deux tableaux à faire un avec 0, 1, 2, 3 et 4
et l'autre de 2,1 à 2,9 puis tu choisis le maximum qui est pour x = 2,8.
-
Eemmxxx dernière édition par