Etude de fonction avec arccos
-
YYB dernière édition par mtschoon
ReBonjour,
Je m'excuse pour avoir mis deux sujets en même temps.
Du coup je reposte le deuxième sujetConsidérons la fonction f définie par : f (x) = arcos (1 − 2x²).
1 Donner l’ensemble de définition Df de f et étudier la parité de f .
2 Calculer f (32)\dfrac{\sqrt{3}}{2} )23) et f (1).
3 Sur quel intervalle maximal, f est-elle dérivable ? Calculer la dérivée de f sur cet intervalle.
4 Montrer que, pour tout réel positif de Df, on a f (x) = 2 . arcsin(x).
En déduire l’allure de la courbe de f sur Df.En attente de votre réponse
-
Bonjour YB,
Ce serait bien si tu indiquais tes éléments de réponse.
Des éléments de réponse à vérifier :- Résoudre −1≤1−2x2≤1-1 \leq 1-2x^2 \leq 1−1≤1−2x2≤1, on trouve x∈[−1;1]x \in [-1 ; 1]x∈[−1;1]
Parité calcul de f(−x)f(-x)f(−x) = ... donc - f(32)=π6f(\dfrac{\sqrt3}{2}) = \dfrac{\pi}{6}f(23)=6π et f(1)=πf(1)=\pif(1)=π.
- fff est dérivable sur x∈]−1;1[x \in ]-1 ; 1[x∈]−1;1[
Sa dérivée : f′(x)=−4x(1−(1−2x2)2f'(x)=\dfrac{-4x}{\sqrt{(1-(1-2x^2)^2}}f′(x)=(1−(1−2x2)2−4x = ....
- Résoudre −1≤1−2x2≤1-1 \leq 1-2x^2 \leq 1−1≤1−2x2≤1, on trouve x∈[−1;1]x \in [-1 ; 1]x∈[−1;1]
-
mtschoon dernière édition par mtschoon

Bonjour YB et Noemi,
Quelques précisions,
La réponse précédente 2) est à vérifier
f(32)=arccos(1−2(32)2)f(\frac{\sqrt 3}{2})= arccos(1-2(\frac{\sqrt 3}{2})^2)f(23)=arccos(1−2(23)2)
donc
$f(\frac{\sqrt 3}{2})=arccos(1-\frac{3}{2})=arccos(-\frac{1}{2})=\fbox{\frac{2\pi}{3}}$La réponse précédente 3) est à vérifier
f n'est pas dérivable pour x=0 car le dénominateur s'annule pour x=0
f est dérivable pour $\fbox{x \in ]-1,0[ \cup ]0,1[}$
Attention aussi au signe de f'(x) qui est à revoir.
Un signe "moins" manque dans la réponse précédente.
Il y a deux signes "-" qui se neutralisent.f′(x)=−−4x(1−(1−2x2)2f'(x)=-\dfrac{-4x}{\sqrt{(1-(1-2x^2)^2}}f′(x)=−(1−(1−2x2)2−4x
$f'(x)=\fbox{\dfrac{4x}{\sqrt{(1-(1-2x^2)^2}}}$
En développant le dénominateur
$f'(x)=\dfrac{4x}{\sqrt{4x^2-4x^4}}=\fbox{\dfrac{2x}{\sqrt{x^2-x^4}}}$
On peut transformer un peu plus, mais en faisant intervenir la valeur absolue ( et en faisant deux cas x>0 et x <0 )
$f'(x)=\dfrac{2x}{\sqrt{x^2}\sqrt{1-x^2}}=\fbox{\dfrac{2x}{|x|\sqrt{1-x^2}}}$
En explicitant et simplifiant
Pour x>0, $\fbox{f'(x)=\dfrac{2}{\sqrt{1-x^2}}}$
Pour x < 0, $\fbox{f'(x)=\dfrac{-2}{\sqrt{1-x^2}}}$
Piste pour la dernière question 4)
Soit g(x)=2arcsin(x)g(x)=2arcsin(x)g(x)=2arcsin(x) pour x > 0
En utilisant la question précédente et en calculant g'(x) on trouve que g'(x)=f'(x)
Donc g(x)=f(x)+C (C constante réelle)
En donnant une valeur simple à x, par exemple 1, on trouver g(1)=f(1) donc C=0 d'où l'égalité cherchée
-
Exact mtschoon,
Réponses un peu rapide de ma part. J'attendais la réaction de YB.
-
mtschoon dernière édition par mtschoon

Effectivement, en allant vite, on peut faire des erreurs.
Tant que j'y suis, je joins un schéma de la fonction f
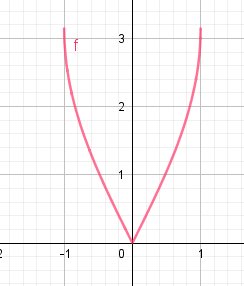
Bon travail YB pour analyser tout ça.
Reposte si tu as besoin.