Fonctions et courbes representatives

[gua]

Bonjour, pouvait vous m'aider

On considère les fonctions définies par
$f(x)=-3x^2+2x+2$
$g(x)=x^2-2x-4$
de courbes représentatives respectives 𝐶𝑓 et 𝐶𝑔

1. Montrer que pour tout nombre 𝑥, on a
   $f(x)-g(x)=-4x^2+5x+6$
2. Développer puis réduire l’expression (4𝑥 + 3)(−𝑥 + 2) afin de montrer qu’elle est égale à 𝑓(𝑥) − 𝑔(𝑥)
3. A l’aide d’un tableau de signes, utiliser la question 2 pour déterminer les
   valeurs de 𝑥 pour lesquelles on a 𝑓(𝑥) − 𝑔(𝑥) > 0 : la solution de cette
   inéquation correspond à l’intervalle sur lequel 𝐶𝑓 se trouve au-dessus de
   𝐶𝑔
4. Dresser le tableau de valeurs des fonctions 𝑓 et 𝑔 sur l’intervalle [−2 ; 3]
   avec un pas de 0,5
5. Sur une feuille de papier millimétré, construire 𝐶𝑓 et 𝐶𝑔. Vous utiliserez
   l’échelle suivante :
    En abscisse : 2cm pour 1 unité
    En ordonnée : 1cm pour 2 unités
6. Par lecture graphique, retrouver les réponses de la question 3

Formules éditées en Latex par la modération.

[mtschoon]

gua bonjour,

Tu n'as rien fait sur cet exercice ?

Je regarde le début.

1)Je suppose que tu as voulu écrire
$f(x)=-3x^2+3x+2$ et $g(x)=x^2-2x-4$

Si c'est bien ça:
$f(x)-g(x)=(-3x^2+3x+2)-(x^2-2x-4)$
$f(x)=g(x)=-3x^2+3x+2-x^2+2x+4$

Après simplification, tu trouves : $f(x)-g(x)=-4x^2+5x+6$

Essaie de poursuivre et tiens nous au courant de ton travail si besoin.

[gua]

@mtschoon non malheureusement j'ai juste réussi a faire le petit 3

[gua]

@gua mais merci quand même tu m'aide énormément

[mtschoon]

Piste pour la 2), si besoin.

Tu développes

$(4x+3)(-x+2)=-4x^2+8x-3x+6=-4x^2+5x+6$

Tu retrouves ainsi l'expression de f(x)-g(x) de la question 1)

Piste pour la 3) si besoin ( je crois que tu l'as faite )

Tu sais que $f(x)-g(x)=(4x+3)(-x+2)$

Tu as fais un tableau de signes :

Une ligne pour x avec les 2 valeurs qui annulent les facteurs, c'est à dire -3/4 et 2
Une ligne pour les signes de (4x+3)
Une ligne pour les signes de (-x+2)
Une ligne pour le signe du produit

Si tu n'as pas fait d'erreur, tu as dû trouver que l'intervalle tel que (4x+3)(-x+2) > 0 est ]-3/4,2[

Reposte si besoin pour la suite de l'exercice.

[gua]

@mtschoon hey merci mais pour le tableau il faut que je fasse 3 lignes 1 pour f(x) 1 autre pour g(x) et une autre pour les intervalle -2, -1.5, -1,-0.5, 0, 0.5, 1, 1.5, 2, 2.5 et 3 c'est ça non?

[mtschoon]

@gua

C'est tout à fait ça.
Tu disposes ton tableau en lignes ou en colonnes

x   \ \    -2 .....
f(x) -16....
g(x) 4......

Evidemment, faire les calculs à la main est fort long !
Si tu as une calculette graphique qui a la fonction TABLE , utilise la.

[mtschoon]

@gua
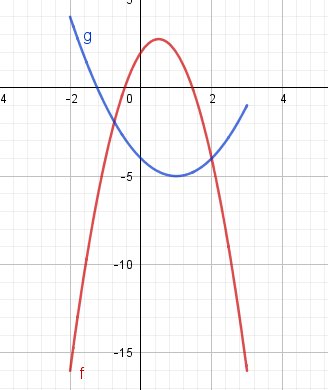
Lorsque tu auras fait le tableau de valeurs demandé à la question 4), avec les points obtenus, il te restera à tracer les courbes et constater que la réponse à la 3) se "voit" bien sur le graphique.

Pour pouvoir vérifier ton schéma, je te joins un graphique (fait avec Geogebra)

Bon travail .