hyperbole (fonction inverse f(x)=1/x)

on considère un point variable M sur la branche de l' hyperbole représentant la fonction inverse définie par f(x) = 1/x sur l’intervalle ]0;+∞[.
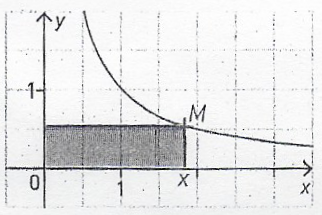
Numérisation_20190301 (2).png
Comment évolue l'aire du rectangle coloré lorsque M se déplace sur la branche d'hyperbole ?

bonjour à tous.
j'ai cet exercice à faire pour la rentrée. Je sais comment l'aire évolue mais je ne sais pas comment l'expliquer correctement. Pouriez-vous m'aider?
merci d'avance.

enzo, bonjour

M a pour coordonnées (x, 1/x)

Pour x >0, les deux dimensions du rectangle teinté sont x et 1/x

Pour tout x >0, l'aire du rectangle est donc $x×1x=...x\times \dfrac{1}{x}=...$ (tu complètes)

@mtschoon
x(1/x)=x/x
Donc l'aire du rectangle est égale à x/x, soit 1.
Donc l'évolution de l'aire du rectangle coloré est constante.

C'est ça ?

Oui, c'est tout à fait ça.

@mtschoon
ok merci à toi.

De rien !
Bon travail.