Exercice Étude de fonction avec racine carrée.

Bonjour aider moi svp
Soit $g(x)=x+2−3x+1g(x)=x+2-\sqrt{3x+1}$
1)a- déterminer Df et calculer lim $g (x)$ en +∞
b- étudier la branche Infinie de la courbe $(C)$ en +∞
2) étudier la dérivabilité à droite de $- 1 / 3$
3)a-montrer que quelque soit $x$ de ]-1/3;+∞[
$g′(x)=(12x−5)/(23x+1(23x+1+3)g'(x)=(12x-5)/(2\sqrt{3x+1}(2\sqrt{3x+1}+3)$
b- dresser le tableau de variation de $g$
4)a- étudier la position de $(C)$ et la droite $(D)$ $y = x$
b-tracer la courbe

Bonjour hafud ,

Piste pour démarrer,

La condition d'existence de g est $3x+1≥03x+1\ge 0$ à cause de la racine carrée.
Tu en déduis Dg

Essaie de poursuivre et propose tes réponses .

Bonjour,

Ce topic n'ayant pas abouti, j'indique des pistes pour consultation éventuelle.

1)a) Vu la condition d'existence, $Dg=[−13,+∞[Dg=\biggl[\dfrac{-1}{3},+\infty\bigg[$

Limite en $+∞+\infty$
Indétermination à lever
On peut mettre x en facteur et prouver que le second facteur tend vers 1 lorsque x tend vers $+∞+\infty$ et déduire ainsi que
$lim⁡x→+∞g(x)=+∞\displaystyle \lim_{x\to +\infty}g(x)=+\infty$

1)b) Avec l'étude faite au 1)a), on peut déduire que :
$lim⁡x→+∞g(x)x=1\displaystyle \lim_{x\to +\infty}\dfrac{g(x)}{x}=1$
La courbe admet donc , en $+∞+\infty$ , une branche parabolique de direction y=x

2)Pour l'étude de la dérivée à droite en $−13-\dfrac{1}{3}$ , on utilise la définition
$lim⁡x→(−1/3)+g(x)−g(−1/3)x−1/3\displaystyle \lim_{x\to (-1/3)^+}\dfrac{g(x)-g(-1/3)}{x-1/3}$
Après calcul, on trouve $−∞-\infty$
Donc g non dérivable à droite pour x= $−13-\dfrac{1}{3}$

3)a) g est dérivable sur $]−13,+∞[\biggl]\dfrac{-1}{3},+\infty\bigg[$

Avec les formules usuelles,
$g′(x)=1−323x+1g'(x)=1-\dfrac{3}{2\sqrt{3x+1}}$

En réduisant au même dénominateur $23x+12\sqrt{3x+1}$ puis en multipliant numérateur et dénominateur par $23x+1+32\sqrt{3x+1}+3$ , puis en transformant le numérateur avec l'identité remarquable (a-b)(a+b)=a²-b², on obtient l'expression proposée par l'énoncé.

3)b) avec l'exopression de g'(x) trouvée, on peut déduire que le signe de g'(x) est le signe de $(12 x - 5$ ) et conclure sur les variations de g

4)a) On doit étudier le signe de g(x)-x , c'est à dire de $(2−3x+1)\biggl(2-\sqrt{3x+1}\biggl)$ sur l'intervalle $[−13,+∞[\biggl[\dfrac{-1}{3},+\infty\bigg[$

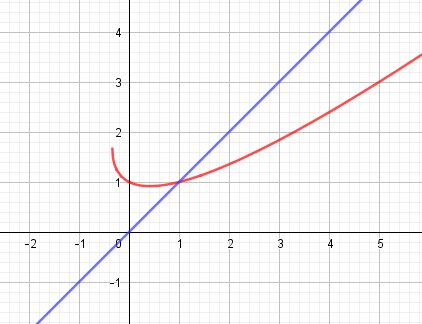
4)b) schéma
(C) est en rouge
(D) d'équation y=x est en bleu
On peut ainsi vérifier les réponses trouvées

@mtschoon pourquoi 3 sur la dérivée du doniminateur

@hafud et pourquoi une branche parabolique de direction y=x

@hafud pour le tableau de variation j'avais trouvé que 12x-5=0 équivalent à x=5/12 mais comment on fait pour le tableau

Bonsoir,
"pourquoi 3 sur la dérivée du doniminateur ?"
Je ne comprends pas ce que tu veux dire...

"pourquoi une branche parabolique de direction y=x"
Car g(x) / x tend vers 1 en + $∞\infty$

Regarde ton cours
Si tu avais g(x) / x qui tend vers a, tu aurais une branche parabolique de direction y=ax (ici a=1)

"pour le tableau de variation j'avais trouvé que 12x-5=0 équivalent à x=5/12 mais comment on fait pour le tableau"

Tu ne sais pas faire un tableau de variation ?
une ligne pour x avec la valeur 5/12
une ligne pour (12x-5) avec - 0 + (qui est le signe de la dérivée)
une ligne pour f avec des flèches correspondant au signe de la dérivée.

@mtschoon mais dans le tableau est ce qu'on ajoute aussi la domaine de définition de fonction f

Oui , dans le tableau, les valeurs de x vont de -1/3 à $+∞+\infty$
(et tu mets 5/12 entre ces deux valeurs-1/3 et + $∞\infty$ )

@mtschoon donc décroissant décroissant croissant

@mtschoon est-ce juste

Non

Décroissant , valeur minimale pour x=5/12 puis croissant.

Observe la représentation graphique pour vérifier tes réponses.

@mtschoon oui

@hafud 4b est-ce qu'on va faire l'encadrement
2>-1/3 et 3x+1>2/3 donc -√(3x+1)>-2/3
D'où 2-√(3x+1)>(-1/3)-(-2/3) c.ad 1/3

" 4b est-ce qu'on va faire l'encadrement"

Revois ta question car dans l'énoncé donné la 4)b) c'est :
"b-tracer la courbe"

Alors ,précise de quelle question tu parles.

@mtschoon c'est 4)a

D'accord . je t'explicite un peu la 4)a)

J'espère que tu as compris qu'il faut , sur l'ensemble de définition, étudier le signe de $g(x)−x=2−3x+1g(x)-x=2-\sqrt{3x+1}$

Je te fais le cas de $\fbox{g(x)-x\gt 0}$ c'est à dire $2−3x+1>02-\sqrt{3x+1} \gt 0$

En transposant le 2, tu obtiens $−3x+1>−2-\sqrt{3x+1} \gt -2$
En changeant les signes (donc le sens de l'inégalité) !
$3x+1<2\sqrt{3x+1}\lt 2$
En élevant au carré (car membres positifs)
$3x+1<43x+1\lt 4$
En terminant simplement cette résolution : $\fbox{x\lt 1}$

conclusion : pour $−13≤x<1-\frac{1}{3} \le x \lt 1$ (C) est au dessus de (D)

Tu traites des cas $g (x) - x = 0$ et $g(x)−x<0\ g(x)-x\lt 0$ avec la même méthode

Comme déjà dit, tu fais la vérification de tes réponses en consultant le graphique.

@mtschoon pour g(x)-x<0 il donne x>1 donc il est au dessus de ∆ et pour g(x)-x=0 il donne x=1 donc il est au dessus de∆ aussi

La droite s'appelait (D) dans l'énoncé, maintenant , elle s'appelle $(Δ(\Delta$ ) ...

J'ignore si tu as compris (???) , mais tes conclusions ne sont pas bonnes

Pour x > 1, (C) est au-dessous de (D)
Pour x=1, (C) coupe (D)

Il faut approfondir tout cela.

@mtschoon c'est une erreur