Etude de fonctions (inverse et cube)

[MATHHHH12]

Bonjour j'ai besoin d'aide pour cet exercice s'il vous plaît car je ne comprend pas :
Soit f la fonction définie sur ]0;+l'infini[ par f(x) = 1/x
Soit C sa courbe représentative dans un repère orthonormal d'unités 1 cm.

1. Tracer la courbe C

A. Calculer f(0,5) et f'(0,5).
B. Tracer la tangente T à la courbe C au point d'abscisse 0,5.
3) Déterminer une équation de T.

Le plan est rapporté à un repère orthonormal d'unités graphiques 4 cm.
Soit f la fonction définie sur [-1;1] par f(x)=x(au cube). Soit C sa courbe représentative dans ce repère.

1. Tracer la courbe C

A. Calculer f(0,5) et f'(0,5)
B. Tracer la tangente T à la courbe C au point d'abscisse 0,5.
3)Déterminer une équation de T.
4) Expliquer pourquoi la tangente T' à la courbe C au point d'abscisse -0,5 est parallèle à T. La tracer.

Merci.

[Noemi]

Bonjour MATHHHH12,

Indique tes éléments de réponse et la question qui te pose problème.
As-tu effectué la représentation graphique ?
$f(0,5)=....$
$f^{\prime }(x)=.....$

[MATHHHH12]

@Noemi

Je n'ai pas d'éléments de réponse ( meme pas le graphique ) parce que je ne comprend vraiment pas

[Noemi]

@MATHHHH12

Pour le graphique, fais un tableau de valeur en prenant par exemple pour
$x$ 1/4 ; 1/2 ; 1 ; 2; 4 calcule
$f(x)$ 4 ; 2; 1; ....
puis construis le repère et place les points.

Indique si tu as réussi à faire le graphique avec ces informations.

[MATHHHH12]

@Noemi

Comment je place les points ?

[Noemi]

@MATHHHH12

$f(x)$ correspond à $y$ l'axe des ordonnées.
point A(1/4 ; 4) , B(1/2;2) .......;

[MATHHHH12]

@Noemi

Pourquoi pour A c'est pas 1/1 ; 1 ?

[Noemi]

@MATHHHH12

Car 1/1 = 1

[MATHHHH12]

@Noemi

Je comprend pas

[Noemi]

@MATHHHH12

Tu ne comprends pas quoi ?

[MATHHHH12]

@Noemi

Ce que vous me demandez

[Noemi]

@MATHHHH12


[MATHHHH12]

@Noemi

B a pour abscisse 0,5 ?

[Noemi]

@MATHHHH12

Oui car 1/2 = 0,5

[MATHHHH12]

@Noemi

f(0,5) = 2 ?

[Noemi]

@MATHHHH12

Oui $f(0,5)=2$

La dérivée est $f^{\prime }(x)=-\frac{1}{x^2}$
calcule $f^{\prime }(0,5)=.....$

[MATHHHH12]

@Noemi

f'(0,5) = -1/0,5au carré =- 1/0,25 = -4 ?

[Noemi]

@MATHHHH12

Oui $f^{\prime }(0,5)=-4$

Pour tracer la tangente, utilise ce coefficient directeur -4.
Pour l'équation de la tangente utilise la relation du cours $y=f^{\prime }(x_0)(x-x_0)+f(x_0)$.

[MATHHHH12]

@Noemi

pour tracerla tangente T a la courbe C au point d'abscisse 0,5 il faut faire comment ?

[Noemi]

@MATHHHH12

Il faut trouver un autre point.
A partir du point B, tu avances de une unité horizontalement puis du descend de 4 unités verticalement, tu places le point correspondant, que tu relies avec le point B.

[MATHHHH12]

@Noemi

Donc quand je decale d'une unité horizontalement j'arrive a 2 en abscisse et quanf je descend de 4 j'arrive a -2 c'est ca ?

[Noemi]

@MATHHHH12

Le point B a pour abscisse 0,5, donc si on avance de 1 unité cela donne 1,5.
L'ordonnée de B est 2, si on descend de 4 unité cela donne -2.
Donc place un point $F(1,5;-2)$ et trace la droite $(BF)$.

Pour l'équation de la tangente, tu remplaces les termes que tu as calculé dans l'équation,
cela donne $y=-4(x-0,5)+2$.
Développe et simplifie cette relation. $y=.....$

Pour la deuxième fonction, tu appliques la même démarche.

[MATHHHH12]

@Noemi

c'est comment pour déterminer l'équation de T?

[Noemi]

@MATHHHH12

Regarde mon post précédent, j'ai ajouté des éléments.

Je te laisse indiquer tes réponses. Je les analyserai demain.

[MATHHHH12]

@Noemi

J'ai développé en distribuant -4 puis j'ai rajouter 2 j'ai trouver -4x+4 mais pas d'equation

[Noemi]

@MATHHHH12

L'équation de la tangente est $y=-4x+4$.

[MATHHHH12]

@Noemi

Pour la deuxième courbe comment faut faire ?

[mtschoon]

Bonjour MATHHHH12 et Noemi,

@MATHHHH12
Noemi t'a aidé à la première question.
Tu dois traiter de la même façon la seconde question.

Pour t'avancer, je te mets un schéma pour la fonction cube

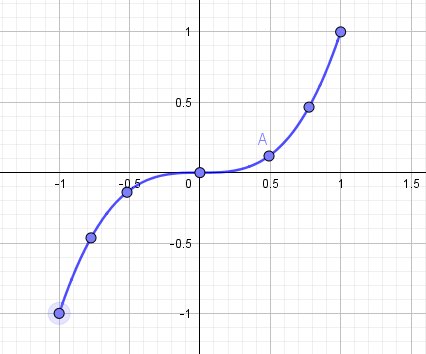
Essaie de poursuivre.

[MATHHHH12]

@mtschoon

Bonjour, j'arrive pas a poursuivre

[mtschoon]

@MATHHHH12

Je te conseille de bien revoir la première question.

Pour poursuivre la seconde :

$f(x)=x^3=x\times x\times x$
$f(0.5)=(0.5{)}^3=0.5\times 0.5\times 0.5=...$ tu comptes

Dérivée usuelle :
$f^{\prime }(x)=3x^2=3\times x\times x$
$f^{\prime }(0.5)=3\times 0.5\times 0.5=...$ tu comptes

[MATHHHH12]

@mtschoon

donc f(0,5) = 0,125
et f'(0,5) = 0,75 ?

[mtschoon]

@MATHHHH12

Oui, c'est ça.

Continue

[MATHHHH12]

@mtschoon pour tracer la tangente T a la courbe c au point d'abscisse 0,5 faut faire comme précédemment ?

[mtschoon]

@MATHHHH12

Tout à fait.
L'équation est ici $y=f^{\prime }(0.5)(x-0.5)+f(0.5)$

Après calculs, sauf erreur, tu devrais trouver $y=0.75x-0.25$

[MATHHHH12]

@mtschoon

mais faudrais que je décale horizontalement de combien ?

[Noemi]

@MATHHHH12

Tu décales horizontalement de une unité et tu montes de 0,75 unité.

[mtschoon]

@MATHHHH12

S tu parles de la dernière question il faut d'abord que tu justifies pourquoi la tangente (T') à la courbe( C) au point d'abscisse -0,5 est parallèle à (T) que tu viens de trouver.

Idée :
Deux droites sont parallèles si et seulement si elles ont même coefficient directeur.
Le coefficient directeur de (T) est $0.75$
Tu calcules le coefficient directeur de (T') qui est $f^{\prime }(-0.5)$ et tu dois trouver pareil.

Ensuite,pour tracer (T'), par le point A' de coordonnées$(-0.5,f(-0.5))$ , tu traces la parallèle à (T) en faisant ce que vient de te dire Noemi

[MATHHHH12]

@mtschoon

A ´ il es placé ou ?

[MATHHHH12]

@Noemi

A partir de A ?

[Noemi]

@MATHHHH12

Si A(0,5 ; 0,125), tu places le point F(1,5 ; 0,875) et tu traces la tangente.

[mtschoon]

@MATHHHH12

Ce n'est pas très clair ...

Si j'ai bien lu, tu as deux tangentes parallèles à tracer.

La tangente (T) relative à la question 2)B) est la tangente en A(05 ,0.125).
Noemi vient de te dire (ou redire, je ne sais plus...) comment la tracer, avec le point F.

Dans la question 4), la tangente (T') est la tangente à la courbe au point d'abscisse -0,5
C'est donc la tangente en A'(-0.5 , -0.125) et cette tangente est parallèle à la tangente (T)

[MATHHHH12]

@Noemi
C'est la tangente T' ?

[MATHHHH12]

@mtschoon

Et j'ai pas compris pour l'explication à la question 4

[mtschoon]

@MATHHHH12

Pour la question 4), relis ma réponse à ce sujet déjà donnée .

RAPPEL :

il faut d'abord que tu justifies pourquoi la tangente (T') à la courbe( C) au point d'abscisse -0,5 est parallèle à (T) que tu viens de trouver.

Idée :
Deux droites sont parallèles si et seulement si elles ont même coefficient directeur.
Le coefficient directeur de (T) est 0.750.75
Tu calcules le coefficient directeur de (T') qui est f'(-0.5)
et tu dois trouver pareil.

Ensuite,pour tracer (T'), par le point A' d'abscisse -0.5 et, tu traces la parallèle à (T)

[MATHHHH12]

@mtschoon Ici avec quel valeur on calcul le coefficient directeur ?

[Noemi]

@MATHHHH12

mtschoon a donné l'indication, pour le coefficient directeur de $(T^{\prime })$ calcule $f^{\prime }(-0,5)$.

[mtschoon]

@MATHHHH12

Et pour calculer $f^{\prime }(-0.5)$ , tu prends $f^{\prime }(x)=3x^2$ et tu remplaces $x$ par -0.5

$f^{\prime }(-0.5)=3\times (-0.5)\times (-0.5)=....$

[MATHHHH12]

@mtschoon D'accord je vous remercie pour votre aide

[mtschoon]

De rien MATHHHH12 et bon travail.