Géométrie dans l'espace indiquer sans justifier les positions relatives des droite et plans dans l'espace

[Sani Ayouba]

Bonjour s'il vous plaît pouvez vous résoudre cet exercice pour moi voici l'énoncé soit le cube ABCDEFGH indiquer sans justifier les positions relatives des droites et plans dans l'espace :1°) des plans EFA et GCD; 2°)des droites EF et HC; 3°) de la droite DG et de plan ABE; 4°)des plans CDF et ABG; 5°) de la droite DF et de plan EHB ; 6°)des droites AG et BH

[mtschoon]

Sani Ayouba bonjour,

Ici, on aide à faire les exercices, mais on ne les fait pas.

J'espère que tu as fait une figure.
Si besoin, je t'en mets une , à compléter au fur et à mesure des questions.
J'espère que les notations sont celles de ton énoncé.

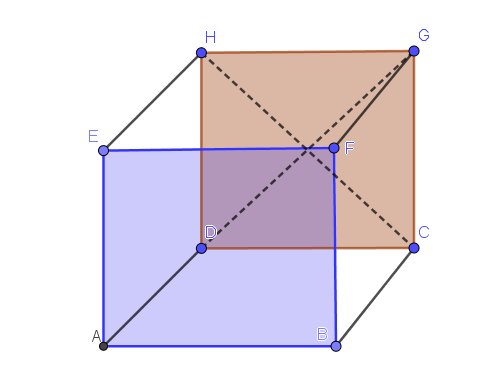
Je te démarre l'exercice.

1. Le plan(EFA) correspond à la face (EFBA) du cube
   Le plan(GCD) correspond à la face (GCDH) du cube

Ces deux plans sont parallèles disjoints.

2. La droite (EF) est dans le plan(EFBA)
   La droite(HC) est dans le plan(GCDH)
   Ces droites sont non coplanaires.
   Elles sont ni parallèles, ni concourantes.

Continue.
Si besoin, donne nous tes réponses et non vérifierons.

[Sani Ayouba]

@mtschoon donc si je comprend pour la suite 3°) comme la droite DG est contenue dans la face DCHG du cube et le plan ABE et contenue dans la face ABCD du cube ça vie dire que la droite DG et sécante au plan ABE vu qu'elle est perpendiculaire à deux droites de ce plan à savoir AE et AB ;4°) VU QUE les plans CDF et ABG se coupent sélection la droite DF qui est leur intersection ça vie dire qu'ils sont sécants ; 5°) la droite DF est parallèle au plan EHB vu qu'elle est parallèle à une droite de ce plan (EH); 6°) les droites AG et BH sont perpendiculaires

[mtschoon]

Regarde bien la figure.

Pour la 3),la droite (DG) est dans le plan ( GCD) parallèle au plan (ABE)

Donc (DG) est parallèle au plan (ABE)

Oui, pour le 4) les plans (EHB) et (ABG) sont sécants

Pour le 5) la droite (DF) coupe le plan(EHB) : (DF) et (EHB) sont sécants.

Pour le 6) dis plutôt que les droites (AG) et (BH) sont sécantes car elles ne sont pas "tout à fait" perpendiculaires.

Bonne lecture dans l'espace.

[Sani Ayouba]

@mtschoon merci beaucoup

[mtschoon]

De rien Sani Ayouba et bon travail !