Limite d'une suite
-
Ssui dernière édition par mtschoon
Bonjour à tous!
J'ai un exercice concernant les fonctions et les suites :
On a fn une fonction définie par fn(x)=e^(-x)+nx sur IR et n appartient à IN*- étudiez les branches infinies de cette fonction ((Cf) admet une branche parabolique de direction de celle de (o,j) au voisinage de +inf et -inf)
- le tableau des variations
- dessinez la courbe de (C2)
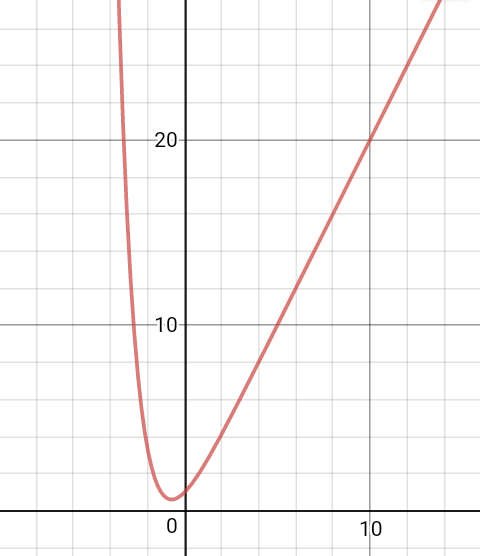
Pour les questions suivantes on a n>=3 - prouver que l'équation fn (x)=0 a deux solutions Un et Vn tel que Un<Vn
(J'ai trouvé que Un appartient à ]-oo,-ln(n)] et Vn appartient à [-ln(n),+oo[ - calculez lim Un et lim Un/ln(n) ( j'ai trouvé que limUn=-inf mais je ne sais pas comment trouver lim Un/ln(n))
Merci d'avance de m'aider !!
-
Ssui dernière édition par
Qu'est ce que vous pensez de cet exercice?
-
mtschoon dernière édition par mtschoon

sui, bonjour,
Ce que je pense de cet exercice ? il est intéressant.
Les réponses que tu donnes sont exactes.
Si j'ai bien compris, il te reste à chercher la limite deUnln(n)\dfrac{U_n}{ln(n)}ln(n)Un lorsque n tend vers +∞+\infty+∞
Pour comprendre le sujet, je mets une représentation graphique avec n=4
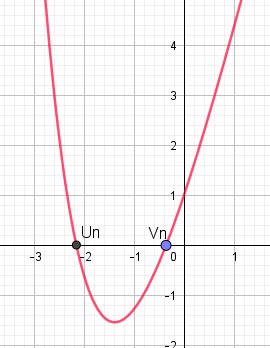
Il faut travailler un peu à" l'inspiration" vu que pour cette dernière question aucune piste ait donnée...
Une idée à tester
Tu sais que f des décroissante sur ]−∞,−ln(n)]]-\infty, -ln(n)]]−∞,−ln(n)]
Tu sais aussi que f(Un)=0f(U_n)=0f(Un)=0 et que f(−ln(n))≤0f(-ln(n)) \le 0f(−ln(n))≤0Tu peux chercher une valeur xnx_nxn inférieure à −ln(n)-ln(n)−ln(n) telle que f(xn)≥0f(x_n) \ge 0f(xn)≥0
Ainsi :
f(−ln(n))≤f(Un)≤f(xn)f(-ln(n)) \le f(Un)\le f(x_n)f(−ln(n))≤f(Un)≤f(xn)xn≤Un≤−ln(n)x_n\le U_n\le -ln(n)xn≤Un≤−ln(n)
Ensuite, tu divises par ln(n) et tu utilises l'encadrement trouvé (théorème des deux gendarmes)
xnln(n)≤Unln(n)≤−ln(n)ln(n)\dfrac{x_n}{ln(n)} \le \dfrac{U_n}{ln(n)}\le \dfrac{-ln(n)}{ln(n)}ln(n)xn≤ln(n)Un≤ln(n)−ln(n)
C'est à dire
xnln(n)≤Unln(n)≤−1\dfrac{x_n}{ln(n)} \le \dfrac{U_n}{ln(n)}\le -1ln(n)xn≤ln(n)Un≤−1
Si f(xn)f(x_n)f(xn) est positive, et si la limite de xnln(n)\dfrac{x_n}{ln(n)}ln(n)xnest égale à -1, la conclusion sera immédiate.
Bien sûr, cela sous-entend de trouver une valeur de xnx_nxn satisfaisante...ce qui n'est pas "évident" !
-
Ssui dernière édition par mtschoon
@mtschoon merci ça va me donner une idée sur la résolution de ce problème !
-
Ssui dernière édition par
J'ai trouvé une manière plus simple:
e^(-Un)=-nUn
<=>-Un=ln(n)+ln(-Un)
<=>-Un/ln(n)=1+ ln(-Un)/(-Un) × (-Un)/ln(n)
<=>(Un/ln(n) )×(-1+ ln(-Un)/(-Un) )=1
<=>Un/ln(n)=1/(-1+ ln(-Un)/(-Un) )
On a : lim (-Un)=+inf
Donc: lim ln(-Un)/-Un =0
Donc : lim Un/ln(n)=-1
-
mtschoon dernière édition par mtschoon

Je regarde ton dernier calcul :
Il est bon et la réponse est bien la bonne.
La limite de Unln(n)\dfrac{U_n}{ln(n)}ln(n)Un lorsque n tend vers +∞+\infty+∞ est bien -1
Effectivement, vu la fonction, trouver une valeur xnx_nxn "à l'aveuglette" n'est pas facile, sauf si on a de la chance .
J'ai fait quelques essais infructueux !
La transformation directe est plus sûre.
Evidemment, il faut savoir un peu ce que l'on veut obtenir pour aboutir...
Bon travail !
-
Ssui dernière édition par
@mtschoon merci pour tes efforts !