Trajet d’une fourmi sur un cube

Bonjour je n’arrive pas à faire cet exercice,

Soit un cube ABCDEFGH de côté : 8cm. On construit le point I tel que BI = 2cm et le point M tel que EM = x cm
Une fourmi est placée au point I, on veut connaître la longueur du trajet de la fourmi pour rejoindre le point H en passant par le point M. On considère que la fourmi se déplace en ligne droite. Elle ne peut se trouver que sur les faces : ABEF et EFGH.

quelles sont les valeurs que peut prendre la variable x ? En déduire l’ensemble de définition Df de la fonction f .
Calculer là longueur IM en fonction de là position M.
calculer la longueur MH en fonction de là position M.
quelle est l’expression de la fonction qui permet de représenter la distance parcourue en fonction de la position de M ?
(énoncé écrit à la main par @Sarah-Martin )

Pour tenter de trouver IM j’avais penser à faire le théorème de Pythagore mais j’ai 2 inconnues et je ne sais pas comment faire, merci d’avance

Sarah Martin , bonjour,

Ici, les scans d'énoncés ne sont pas autorisés (sauf les graphiques et tableaux de nombres)

Merci d'écrire ton énoncé à la main

@mtschoon bonjour, désolé mais je n’avais vu nul part que cela était interdit

Pas de problème, Sarah Martin

Nous attendons ton énoncé écrit.

Tu peux scanner le graphique.

@Sarah-Martin , re-bonjour

Je viens de te faire une image du cube pour le cas où tu ne serais pas arrivé(e) à le scanner sans le texte.
.

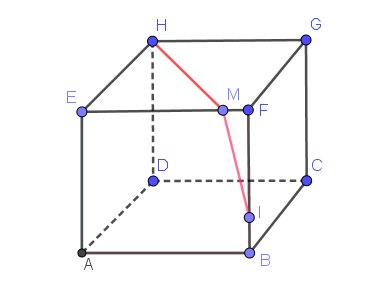Su tu as besoin d'aide, écris l'énoncé, sinon tant pis...

@mtschoon bonjour merci beaucoup, je vais réécrire l’énoncé pour que l’on puisse m’aider , merci encore

Bonjour, je n’arrive pas trop à faire cette exercice ci-dessous. Pourriez vous m’aider s'il vous plait ?
Merci d’avance.

Dans cette partie on étudie la fonction définie sur l'intervalle [ 0 ; 8 ] et qui a pour expression : f(x) = √ x² + 64 + √ x²- 16x+100

Remplir ce tableau de valeur a l'aide de la calculatrice : J'ai trouver ceci x=0 f(x) = 18 ; x=1 f(x) ≈ 17,30 ; x=2 f(x)≈16,74 ; x=3 f(x)≈ 16,35 ; x= 4 f(x)≈16,16 ; x= 5 f(x)≈ 16,15 ; x=6 f(x) ≈ 16,32 ; x=7 f(x) ≈ 15,53 ; x=8 f(x) ≈ 17,31. Mais je ne suis pas sur de moi
Remplir ce tableau de variation : x 0 7 8
f(x) 18 Flèche qui descend vers le bat jusqu'à 15,53 ensuite flèche monte vers le haut a 17,31. Mais je ne suis vraiment pas sur de moi
Dans un repère orthonormée ( prendre OI = 1cm), tracer la fonction f . J'ai tracer ma fonction par rapport a mon tableau de valeur mais sa me une courbe etrange. Donc je ne comprend pas.
La fourmi étant paresseuse elle veut savoir par ou doit passer son chemin pour effectuer le trajet le plus court possible. D'après les résultat precedent quelle doit etre la longueur minimale ? Dans ce cas quelle est la longueur que devra parcourir la fourmi ?

Bonsoir Sarah-Martin,Thibault Picardet

Thibault Picardet , tes questions doivent être faites après la partie relative à la fourmi que Sarah-Martin viens d'écrire...

@Sarah-Martin
Merci d'avoir écrit ton énoncé à la main.

Pistes pour la partie relative à la fourmi
$0≤x≤80\le x\le 8$
Avec le théorème de Pythagore
$IM^2=IF^2+FM^2=(8-2)^2+(8-x)^2$
après calculs
$IM=x2−16x+100IM=\sqrt{x^2-16x+100}$

$MH^2=ME^2+EH^2=x^2+8^2$
après calculs
$MH=x2+64MH=\sqrt{x^2+64}$
d'où $f(x)=IM+MH=x2+64+x2−16x+100f(x)=IM+MH=\sqrt{x^2+64}+\sqrt{x^2-16x+100}$

@Thibault-Picardet

Pour le tableau de valeurs ; tout est bon sauf pour x=7
Vérifie : $f(7)≈16.71f(7)\approx 16.71$

2)Globalement c'est bon, mais il faut modifier le minimum qui n'est pas pour x=7 à cause de ton erreur précédente.

C'est peut-être ton erreur pour x=7 qui te fausse la courbe

Je te joins un schéma

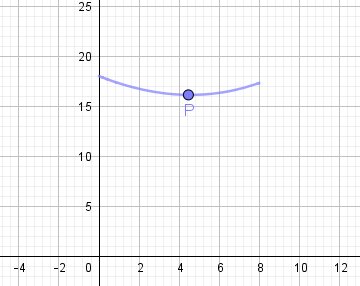
Pense au point P que j'ai indiqué qui correspond à la valeur minimale de f(x)

@mtschoon merci beaucoup !!

@mtschoon merci pour votre réponse, je pense que pour la courbe c’est parce que je la fais à la main et étant donner que les valeurs sont décimal, c’est donc pas pointilleux.

De rien !

@Sarah-Martin
Reposte si tu n'arrives pas bien à trouver f(x)

@Thibault-Picardet
Effectivement, les valeurs décimales n'arrangent pas pour le graphique...
J'ai fait le schéma avec Geogebra.
Si tu as une calculatrice graphique, tu peux faire tracer la courbe à ta calculatrice pour te faire une idée.

Bon travail à tous les deux.

@mtschoon merci beaucoup je vais continuer avec ces informations là, encore merci

@mtschoon excusez moi mais pour vous la question 4 la longueur EM est égale 3 ou 5 ?

@Sarah-Martin
Pour la 4), il s'agit toujours de la longueur IM=f(x) et non de la longueur EM.

Il faut indiquer la position de M, donc la valeur de x, pour que la longueur IM soit minimale.

IL faut donc regarder le tableau de variations de f qui correspond au tableau de valeurs.

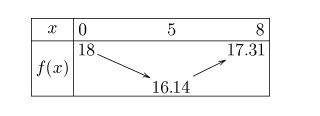
@Thibault-Picardet a proposé x=7 car il a fait une faute de calcul.
Si tu observes bien, le minimum (qu'il faut indiquer dans le tableau de variations) est pour x=5 et $f(5)≈16,14f(5)\approx 16,14$
Donc, la longueur minimale est environ $16.14$
La précision dépend de la calculatrice . La mienne me donne $16.142$
Utilise ce que donne la tienne.
C'est donc cela la longueur du trajet si la fourmi est paresseuse.

Une remarque (non demandée dans l'énoncé)
L'étude est basée sur le tableau de valeurs de x.
Si on avait demandé plus de précisions ( par exemple des valeurs de x à 0.1 près ou à 0.01 près) on aurait trouvé que le minimum se situe plus précisément entre $4.5$ et $4.6$ et que la valeur minimale était environ $16.125$ .

Vu l'énoncé proposé, c'est $x = 5$ qu'il faut prendre pour obtenir le minimum de f (mais ce n'est qu'une valeur approchée)

@mtschoon ah d’accord merci beaucoup, c’est à dire que la longueur EM est égale à 5cm ce qui fait que MF est égal à 3cm

Si tu parles du cas demandé à la question 4) :
Oui x=5 et comme EM=x, effectivement dans ce cas EM=5 et MF=8-5=3

@mtschoon Bonjour,

On se propose de tracer le parcours de la fourmi sur le patron de ce cube
Reproduire ce tableau à une échelle que vous définirez.
Placer le point M tel que dans le cube réelle la distance EM= 6cm
donc pour cette question je pense placer le point M sur la longueur EF de longeur EM= 6cm et donc MF= 2cm.
Mesurer la longueur parcourue par la fourmi. Retrouve t-on les résultats du II 1) ?
Donc je pense que la longueur parcourue par la fourmi est de 16,32 cm. On ne trouve donc pas les résultats du II car étant donner que EM n'est pas égal a la même longueur que le II.
Selon vous quel doit être le chemin suivi par la fourmi pour minimiser la distance parcourue . Placer le point M1 correspondant et mesurer la distance EM1. Retrouve t-on les resultats obtenus précédemment ?
Et pour cette question je n'y arrive pas du tout.
MERCI d'avance. Bonne journée.

@mtschoon d'accord merci beaucoup

@Sarah-Martin
C'est bien, vu que c'est tout à fait la question que tu posais.

@Thibault-Picardet

Je suppose que tu as fait le patron.

Oui, pour la 2) : EM=6 . vu que EM=x, ici x=6 et tu dois retrouver la longueur f(6)=16.32

Pour la 3), pour minimiser la distance parcourue, tu pourrais bien sûr placer le point M dans la position M1 telle que EM1=x=5 pour voir ce qui se passe, conformémént à la question précédente.
Dans cette position tu dois retrouver que la longueur du chemin vaut f(5), c'est à dire 16.14 (qui est la valeur minimale indiquée dans le tableau pour le chemin parcouru) mais graphiquement ce n'est pas véritablement le chemin le plus court.

Avec le patron, tu dois constater qu'il y a une meilleure position pour M1.
C'est cela qu'il faut trouver.

@mtschoon Bonsoir, merci pour votre réponse. Mais je ne comprend pas totalement.

On se propose de tracer le parcours de la fourmi sur le patron de ce cube
Reproduire ce patron à une échelle que vous définirez.
Je ne comprend pas bien comment je peux tracer le parcours de la fourmi sur le patron de ce cube. Dois-je tracer le parcours le plus petit, a partir du point I, Passant par le point M qui coupe l'arrête EF en EM= 5cm et en se terminant au point H en sachant que la fourmi traverse seulement les faces ABFE et EFGH ?
Placer le point M tel que dans le cube réelle la distance EM= 6cm.
je dois donc tracer EM=6cm sur l'arrête EF ?
Mesurer la longueur parcourue par la fourmi. Retrouve t-on les résultats du II 1) ?
Est-ce que on doit mesurer la longueur parcourue par la fourmi avec une règle ? Et si c'est le cas sur la règle est-ce qu'il faut regarder 16cm et 3mm pour trouver 16,32 ?
Selon vous quel doit être le chemin suivi par la fourmi pour minimiser la distance parcourue . Placer le point M1 correspondant et mesurer la distance EM1. Retrouve t-on les resultats obtenus précédemment ?
Le point M1 je le met donc sur l'arrête EF de longueur EM1 = 5cm sur le patron ? Je ne comprend la question " Retrouve t-on les resultats obtenus précédemment ?"

Pourriez-vous m'aider s'il vous plaît ? Merci d'avance

@Thibault-Picardet

En bref, c'est le patron qui te pose problème.
(Tu aurais dû le dire précédemment)

Je te joins un schéma où le patron est fait à partir de la base ABCD
J'espère que tu va comprendre les notations utilisées.
Prends le temps d'y réfléchir.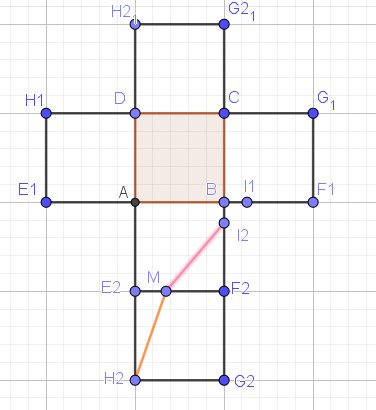

Quelques indices utiles pour répondre aux questions :

$E_2M=x$
$BI_1=BI_2=2$
$f(x)=I_2M+MH_2$ (chemin de la fourmi, en rouge)
Tu fais toutes les mesures à la règle
Le chemin le plus court est la ligne droite

Je ne t'en dis pas plus.
J'espère qu'avec les indices donnés tu pourras répondre aux questions.

@mtschoon Bonjour, excusez-moi de vous déranger.
J'ai encore des difficultés pour effectuer cette exercice. Pourriez vous m'aider a confirmer les réponses que je viens de trouver s'il vous plait ?
Voici :

J'ai réaliser le patron de ce cube. J'ai donc tracer le parcours le plus court c'est à dire EM=5cm, cela m'a donc donné une mesure de 16,2 cm à la règle au lieu de 16,15 sur le tableau de valeur du II. Je pense que on peut dire que l'on retrouve les même résulats.
Pour cette question je pense avoir bon : j'ai placer le M sur le côté EF avec EM=6cm.
J'ai donc mesurer la longueur parcouru par la fourmi pour EM=6cm. En mesurant à la règle j'ai trouver 16,4 cm au lieu de 16,32 cm mais je pense que l'on peut dire que l'on retrouve les résultats du II 1). N'est-ce pas ?
J'ai répondu que selon moi le chemin suivi par la fourmi pour minimiser la distance parcourue est le chemin de EM=5cm. Sur le patron, j'ai donc placer le point M1 de mesure EM=5cm donc la distance EM1=5cm.
On retrouve les résultats obtenus précédemment, mais je ne suis pas sur pour ça car je ne comprend peut être pas bien la question. Le mot précédemment se refère t-il a l'exercice II ou de la question 3 de l'exercice III ?
Merci pour votre aide. Bonne journée.

@Thibault-Picardet

Effectivement, tu ne maîtrises pas encore la totalité.

On te demande seulement le patron et le chemin de la fourmi.
Tu fais donc un patron comme le schéma joint, en plaçant M sur le bon segment (c'est tout)
Tu places cette fois M tel que EM=6
Sur le patron tu places donc M tel que $E_2M=6$
Ta mesure me semble bonne
Ta réponse est à revoir.
Regarde le patron
La longueur du chemin de la fourmi (en rouge) est $I_2M+MH_2$
Comme je te l'ai indiqué, le chemin le plus court est la ligne droite.
Donc le chemin le plus court est lorsque $I_2,M,H_2$ sont alignés.
En bref, tu traces à la règle, le segment $I_2H_2]$ qui va couper le segment $E_2H_2]$ au point $M_1$
Tu fais les mesures avec cette situation qui est la meilleure (ce sera la véritable réponse pour le chemin le plus court)

Enfin, à la question "retrouve-on les résultats obtenus précédemment (c'est à dire pour x=5) ?" , tu dois répondre NON et expliquer pourquoi.

@mtschoon Bonsoir, je n'ai pas très compris la réponse "NON" de la question 4 puisque en mesurant le parcours de la fourmi par rapport a EM1= 5cm, ça me donne 16,2 cm en mesurant sur le patron mais sur le tableau de valeur on trouve environ 16,15 cm, donc pour moi je pensais que l'on retrouvait les résultats obtenus avant.
Pourriez-vous me dire pourquoi vous répondriez que "NON" ?

@Thibault-Picardet

Théoriquement, il y a une petite différence (seulement petite)

Lorsque tu places M1 de façon que les points $I_2,M,H_2$ soient alignés, indique la valeur de $x=E_2M$ correspondante que tu as mesurée.
Tu devrais logiquement trouver une valeur légèrement inférieure à 5

Si tu préfères, pour $x = 5$ , les points $I_2,M,H_2$ ne sont pas tout à fait alignés.

Evidemment, les différences sont légères vu que x=5 est une valeur approchée de la valeur de x correspondant au "minimum exact"que tu trouves graphiquement en plaçant $M_1$ sur le patron.

Je pense que c'est cette "nuance" que ton énoncé veut te faire trouver.

Je te rappelle la remarque que j'ai indiqué précédemment, vers le début de cette discussion :
"Une remarque (non demandée dans l'énoncé)
L'étude est basée sur le tableau de valeurs de x.
Si on avait demandé plus de précisions ( par exemple des valeurs de x à 0.1 près ou 0.01 près) on aurait trouvé que le minimum se situe plus précisément entre $4.5$ et $4.6$ et que la valeur minimale est environ $16.125$ "

Bonsoir, merci pour votre réponse.
je vous récapitule tout ce que j'ai répondu pour cette exercice pour être certain que je ne me suis pas trompé sur quelques choses.

J'ai construit un patron identiques au mesure du sujet.
J'ai tracé le chemin de la fourmi par rapport à EM=5cm
J'ai placer le point M sur le côté EF tel que EM= 6cm
J'ai mesuré la longueur parcourue par la fourmi par rapport a EM=6cm et sa me donne 16,4 cm à la règle. Donc on retrouve les résultats du II 1) car 16,32 afficher au tableau de valeur c'est un peu près identiques à 16,4 cm.
Selon moi le chemin suivi par la fourmi pour minimiser la distance parcourue il faudrait qu'elle traverse du point I passant par M et se terminant en H en ligne droite. J'ai placé le point M1 dès que la droite coupe EF, après j'ai mesuré EM1 donc EM1= 4,6 cm. Oui on retrouve les résultats obtenus précédemment car même si il y a 0.1 unité près donc oui c'est le même résultat étant donné que le parcours minimal sur le tableau de valeur est de 16,15cm, et j'ai mesurer 16,125 cm en fonction de EM=4,6 cm. Alors 16,15 et 16,125 c'est un peu près la même chose.
Pourriez-vous me donner confirmation de mes réponse ?
MERCI beaucoup pour m'avoir aider.
Bonne soirée.

@Thibault-Picardet

Globalement, c'est bon, mais la fin de la 4) ne me convient toujours pas parfaitement...
$\approx 16.125$
$f(5)≈16.15f(5)\approx 16.15$

Pour x voisin de 4.6, les 3 points sont alignés : c'est le trajet le plus court (16.125 environ)
Pour x=5, les 3 points ne sont pas alignés; le trajet est forcément un peu plus long (16.15 environ)

C'est ce que tu dois trouver si tu fais les calculs à la calculette.
En mesurant, ce serait bien que tu trouves à peu près pareil...

Comme $\lt 16.15$ , le minimum le plus précis est pour $x≈4.6x\approx 4.6$ et non pour $x = 5$

C'est un détail, certes, mais ce serait bien que tu l'indiques et cela justifierait l'intérêt d'avoir fait un patron pour avoir le point $M_1$ précis.

@mtschoon D'accord, merci.
Donc je dois répondre : Selon moi le chemin suivi par la fourmi pour minimiser la distance parcourue il faudrait qu'elle traverse du point I passant par M et se terminant en H en ligne droite. J'ai placé le point M1 dès que la droite coupe EF, après j'ai mesuré EM1 donc EM1= 4,6 cm. Oui on retrouve les résultats obtenus précédemment car en calculant a la calculatrice par rapport à x= 4.6 cm, sa donne environ 16,125 cm et avec x = 5cm , sa donne environ 16,15., et en mesurant a la règle sur le patron pour EM= 4,6cm sa donne 16,1 cm et pour EM=5cm sa donne 16,1 cm, alors on peut dire que on retrouve bien les résultats obtenus précédemment. Donc on peut remarquer en calculant à la calculatrice que le minimum le plus précis est pour x≈4.6 cm et non pour x=5 cm. ?

@Thibault-Picardet
C'est ton professeur qui juge, pas moi, bien sûr, mais cette fois, il me semble que l'idée y est.
Bon travail !

@mtschoon merci beaucoup d'avoir pris le temps de m'aider. Bonne fin de soirée.

@Thibault-Picardet , de rien et continue à bien travailler.