Isomorphisme - bijection

Bonjour tout le monde j'espère que vous allez bien !
J'ai pas un exercice spécifique mais une simple question concernant les structures algébriques; ma question est comment on peut prouver qu'un morphisme est bijectif, pour les fonctions c'est facile on peut tout simplement montrer que la fondation est continue et strictement positive mais quand on a un couple comment on peut le faire ?
Par exemple ici on a

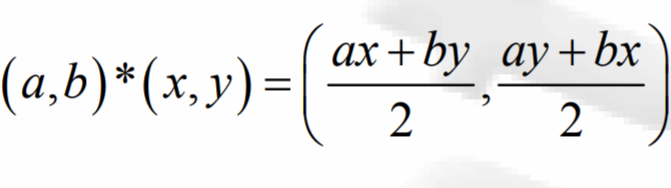
On considère que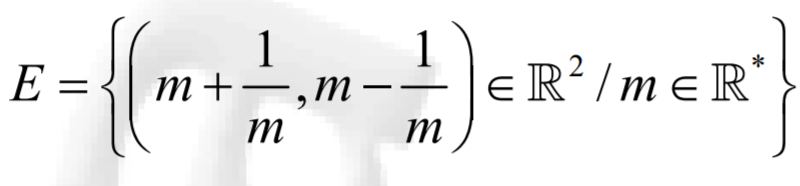
j'ai prouvé que * est une loi de composition interne sur E (question1)

(2) (phi) est une application de IR* à E tel que :
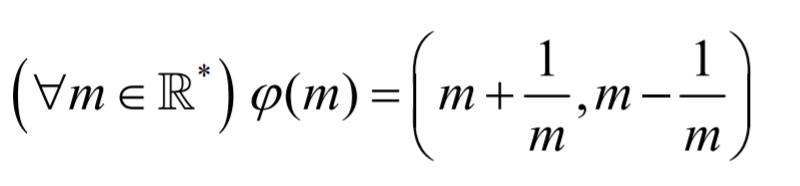
Ici je dois prouver que (phi) est un isomorphisme de (IR*;×) À (E,*) ici je ne sais pas comment répondre j'ai prouver que : phi(m)*phi(n)=phi(mn) mais il me reste de monter que c'est bijectif
Et s'il vous plaît si vous connaissez une méthode avec laquelle je peux résoudre des exercices comme celle-ci partagez la avec moi, ça va m'aider beaucoup !
(Désolé pour ne pas écrire en LaTex j'ai essayé mais ça ne marche pas avec moi...)
Merciiiii

@sui , bonjour,

Je regarde un peu ta question.

Si j'ai bien lu, tu as déjà démontré que $φ\varphi$ est un morphisme de (R \ {0} , $×\times$ ) vers (E , * )
c'est à dire que pour pour tout m réel non nul et tout n réel non nul
$φ(m×n)=φ(m)∗φ(n)\boxed{\varphi(m \times n)=\varphi(m) * \varphi(n)}$

Il te reste à démontrer que $φ\varphi$ est une bijection de R \ {0} vers E

Pour cela, tu peux prouver que tout élément y de E a un antécédent x unique dans R \ {0} , c'est à dire qu'il existe un élément x réel non nul unique tel que $φ(x)=y\varphi(x)=y$

Piste ,

Soit y un élément quelconque de E
D'après la définition de E, y s'écrit
$y=(m+1m,m−1m)y=(m+\dfrac{1}{m},m-\dfrac{1}{m})$ avec $\in$ R \ {0}

On cherche donc x réel non nul tel que $φ(x)=(m+1m,m−1m)\varphi(x)=(m+\dfrac{1}{m},m-\dfrac{1}{m})$ , c'est à dire :

$(x+1x,x−1x)=(m+1m,m−1m)(x+\dfrac{1}{x},x-\dfrac{1}{x})=(m+\dfrac{1}{m},m-\dfrac{1}{m})$ ,

c'est à dire
${x+1x=m+1mx−1x=m−1m\boxed{\begin{cases} x+\dfrac{1}{x}=m+\dfrac{1}{m} \cr \cr x-\dfrac{1}{x}=m-\dfrac{1}{m}\end{cases}}$

Tu dois donc résoudre, à la façon de ton choix, ce système d'inconnue x (m servant de paramètre) et tu dois trouver que la solution unique est x=m

Merci @mtschoon cette exactement ce que j'ai voulu dire,
Je vois que en additionner
$x+1x=m+1m{x+\dfrac{1}{x}=m+\dfrac{1}{m}}$
et
$x−1x=m−1m{x-\dfrac{1}{x}=m-\dfrac{1}{m}}$
On va trouver ${x=m}$
Donc avec cette méthode que je peux répondre à ce type de questions (c'est un peu aussi comme les fonctions je vois )

@sui ,

Oui, en ajoutant membre à membre, on trouve donc que x=m
Ceci est la "partie directe" de l'explication.
Si c'était un devoir à rendre, en toute rigueur, il faudrait compléter l'explication, en indiquant "la partie réciproque" (qui est ici évidente) : Pour x=m, les deux équations sont bien satisfaites.

Effectivement, les définitions de bijections, injections, surjections d'un ensemble E vers un ensemble F sont générales.
Elles ne dépendent pas de la nature des ensembles E et F considérés.

Merciii @mtschoon

De rien @sui et bon travail !