Aide Dm de maths Fonction-Volume d'un cube
-
Sshana67 dernière édition par mtschoon
Bonjour j’ai un devoir maison a rendre mais une question me pertube je ne suis pas sur du resulat
Exercice :
On dispose d’une feuille de dimension 21cm x 29,7 cm avec laquelle on veut fabriquer une boite sans couvercle. Pour cela on decoupe aux 4 coins de la feuille un carré de côté x. On obtient le patron de la boite. On se propose d’etudier le volume de la boite en fonction de x.- quelles sont les valeurs possibles pour x?
Ma reponse: comme x>0 et que les côtés de la feuilles valent 29,7-2x et 21-2x
Alors 29,7-2x>0
X>14,85
21-2x>0
X>10,5
Donc les valeurs possibles pour x sont ]0;10,5[ et ]0,14,5[
C’est juste? - on appelle v(x) le volume de la boite
a) montrer que v(x)=4x^3-101,4x^2+623,7x
Ma reponse: volume rectangle = l.L.h
Longueur= 29,7-2x cm largeur= 21-2x cm h = x
x(29,7-2x)(21-2x) et en developpant je retombe sur v(x)
b) etudier les variations de V
J’ai calculé la dérivée
V’(x)= 12x^2-202,8x+623,7
J’ai calculé delta qui vaut 11190,24 c ici que je trouve que c’est bizarre ( si qlqn peut me corriger)
Et je trouve que la courbe est croissante de - l´infini a environ 4,04 puis decroissante de 4,04 a environ 13 et croissante de 13 a + l’infini ( ce sont des valeurs approchés)
C) en deduire la ou les valeurs de x pour laquelle / lesquelles le volume de la boite est maximum
Ma reponse: maximum pour x envrion egale a 4,04
C’est juste ?
- quelles sont les valeurs possibles pour x?
-
mtschoon dernière édition par mtschoon

shana67, bonjour,
Je regarde tes réponses.
- A revoir car erreur dans le sens des inégalités.
(lorsqu'on divise par un nombre négatif, on change le sens de l'inégaliré)
Nécessairement x > 0
29.7-2x > 0 <=> -2x > -29.7 <=> x < (-29.7)/(-2) <=> x <14.85
21-2x > 0 <=> -2x > -21 <=> x < (-21)/(-2) <=> x < 10.5{x<14.85x<10.5\begin{cases}x \lt14.85\cr x\lt 10.5\end{cases}{x<14.85x<10.5<=> x<10.5x\lt 10.5x<10.5
Conclusion : 0<x<10.5\boxed{0 \lt x \lt 10.5}0<x<10.5
Remarque : tu peux , si tu préfères, mettre les inégalités au sens large, si tu souhaites englober les les deux cas limites où le volume sera nul. 0≤x≤10.5\boxed{0\le x \le 10.5}0≤x≤10.5
2)a) c'est bon
2)b) : tes confusions viennent de l'erreur au 1)
Tu dois étudier les variations de V sur [0,10.5]
V croissante sur [0, 4.04]
V décroissante sur [4.04, 10.5]
Maximum égal à 1128.5 pour x=4.04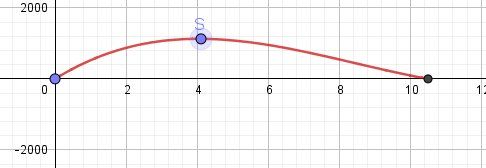
- A revoir car erreur dans le sens des inégalités.