Le disque unité (explication ) et produit cartésien
-
Ssui dernière édition par mtschoon
Bonjour tout le monde!
J'ai étais en train de résoudre les questions d'un concours mais j'ai trouvé une question dont je ne sais pas la réponseVoilà la question

S'il vous plaît peut quelqu'un m'expliquer c'est quoi un disque d'unité, j'ai cherché sur internet, j'ai trouvé seulement la page de Wikipedia, mais il n'était pas clair pour moi!
Merci d'avance!
-
mtschoon dernière édition par mtschoon

@sui , bonsoir,
Dans une repère orthonormé d'origine 0, D est le disque"fermé", limité par le cercle de centre 0 et de rayon 1
Le cercle de centre O et de rayon 1 a pour équation x²+y²=1
La zone à l'intérieur de ce cercle a pour équation x²+y² < 1
Le disque (il s'agit ici du disque" fermé" composé du cercle et de son intérieur) a donc pour équation x2+y2≤1x^2+y^2 \le 1x2+y2≤1
-
Ssui dernière édition par sui
Bonsoir @mtschoon
J'ai compris maintenant ce qui est un disque d'unité, Merci infiniment!
Mais la proposition reste incompréhensible, est-ce que vous pouvez me l'expliquer !
-
mtschoon dernière édition par mtschoon

La proposition P veut dire qu'il existe deux parties A et B de R telle que A x B=D
Par définition, A x B (produit cartésien de A par B) est l'ensemble de tous les couples (x,y) tels que
x appartient à A et y appartient à B.Cette proposition P est fausse.
Pour le prouver, tu peux faire un raisonnement par l'absurde en utilisant les couples (0,1) et (1,0) dont te parle l'énoncé et trouver une contradiction.
Essaie.
-
mtschoon dernière édition par mtschoon

@sui , re-bonjour,
Je t'indique quelques pistes si tu as besoin
Illustration graphique (seulement pour comprendre)
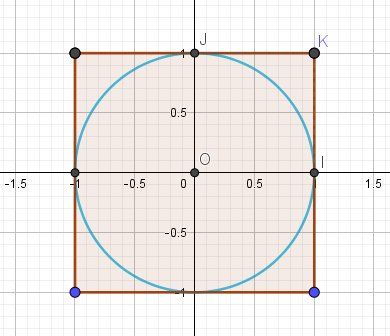
Détail du raisonnement par l'absurde en utilisant les données (1,0) coordonnées de I et (0.1) coordonnées de J.
(0.1)∈D(0.1) \in D(0.1)∈D car 02+12≤10^2+1^2 \le 102+12≤1 ( plus précisément, 02+12=10^2+1^2 = 102+12=1 (point J sur le cercle)
De même
(1.0)∈D(1.0) \in D(1.0)∈D car 12+02≤11^2+0^2 \le 112+02≤1 ( plus précisément, 12+02=11^2+0^2 = 112+02=1 (point I sur le cercle)Vu l'hypothèse D=A x B,
(0,1)∈A×B(0,1)\in A \times B(0,1)∈A×B et (1,0)∈A×B(1,0) \in A \times B(1,0)∈A×BAvec la définition de A×BA \times BA×B, on peut déduire que :
$\fbox{0\in A}$ et $\fbox{1\in B}$ et $\fbox{1\in A}$ et $\fbox{0\in B}$Conséquence:
Vu que 1∈A1\in A1∈A et 1∈B1\in B1∈B , nécessairement (1,1)∈A×B(1,1)\in A \times B(1,1)∈A×B
Vu l'hypothèse A×B=DA \times B =DA×B=D, on déduit que (1,1)∈D(1,1)\in D(1,1)∈DCela est impossible vu que le point K de coordonnées (1,1) n'est pas dans D
Preuve pour être rigoureux :
12+12≤11^2+1^2\le 112+12≤1 est FAUX car 12+12=21^2+1^2=212+12=2L'hypothèse D=A×BD=A \times BD=A×B est donc fausse
CQFD.
-
mtschoon dernière édition par mtschoon

Tant que j'y suis, je t'indique une autre version qui me vient à l'esprit.
Je ne pense pas que ça soit l'idée prévue par l'énoncé vu qu'elle n'utilise par (0,1) et (1,0).
Elle est peut-être plus simple à comprendre mais plus difficile à traiter avec rigueur.Observons D :
Pour tout point de coordonnées (x,y) de D : −1≤x≤1-1\le x \le 1−1≤x≤1 c'est à dire x∈[−1,1]x\in [-1,1]x∈[−1,1]
Pour tout point de coordonnées (x,y) de D : −1≤y≤1-1\le y \le 1−1≤y≤1 c'est à dire y∈[−1,1]y\in [-1,1]y∈[−1,1]
Donc, d'après la définition du produit cartésien:
(x,y)∈[−1,1]×[−1,1](x,y) \in [-1,1] \times [-1,1](x,y)∈[−1,1]×[−1,1]Les deux seules valeurs de A et B à étudier sont donc
A=[−1;1]A=[-1;1]A=[−1;1] et B=[−1,1]B=[-1,1]B=[−1,1]
Les valeurs de A×BA \times BA×B sont les coordonnées des points du carrée en rouge sur le graphique (avec son intérieur).Mais alors, l'égalité D=A×BD=A \times BD=A×B est fausse.
Il suffit bien sûr de regarder le graphique , mais on peut le justifier rigoureusement en utilisant K (1,1)
(1,1)∈A×B(1,1)\in A \times B(1,1)∈A×B (K est un sommet du carré)
(1,1)∉D(1,1) \notin D(1,1)∈/D vu que 12+12≤11^2+1^2\le 112+12≤1 et faux (K est à l'extérieur du disque)Conclusion :
l'égalité D=A×BD=A \times BD=A×B n'est pas exacte.J'espère @sui, qu'une de ces deux explications, ou les deux, te conviendront...
Bonne lecture et bonne préparation à ton concours .
-
Ssui dernière édition par
Merci beaucoup @mtschoon !



J'ai bien compris la deuxième explication .
-
mtschoon dernière édition par

De rien @sui et très contente de t'avoir été utile !
