Probabilité - notion d'indépendance
-
Ddut dernière édition par
Bonjour j'essaie de comprendre un cours du net sur les probas mais je ne suis pas sûr de comprendre l'indépendance d'événements.
Lançons deux dés, et considérons les deux événements : A=«la somme des deux chiffres obtenus est paire» et B=«le 1ou le 2 sort au moins une fois». Les événements A et B sont-ils indépendants ?
Pour commencer j'ai représenté les couples possibles -> j'en ai trouvé 21
Événement A = 12/21
Événement B = 10/21Je ne sais pas comment conclure avec ça sur l'indépendance d'événement
Merci
-
Bonjour dut,
Tu appliques :
Deux événement sont indépendants si et seulement si
P(A∩B)=P(A)×P(B)P(A\cap B) =P(A)\times P(B)P(A∩B)=P(A)×P(B)
-
Ddut dernière édition par
Bonjour Noemi,
Merci pour la formule.
Ca veut dire que si les 2 événements sont indépendants alors je peux faire 12/21 * 10 /21
Je ne vois juste pas comment ce produit me permet de savoir si il y a indépendance
-
Calcule : P(A∩B)P(A\cap B)P(A∩B)
-
Ddut dernière édition par
Je trouve pour l'union 6/21 soit 0,2857
P(A)*P(B)= 12/21 * 10/21 = 0,2721
-
Tu dois calculer : P(A∩B)P(A\cap B)P(A∩B) en utilisant la relation :
P(A∩B)=P(A)×PA(B)P(A\cap B) =P(A)\times P_A(B)P(A∩B)=P(A)×PA(B)
ou en considérant que :
A∩BA\cap BA∩B est constitué des éventualités qui appartiennent à la fois à A et à B.
-
Ddut dernière édition par
Que veut dire PA(B)?
(A∩B) -> représente les 2 événements simultanément
P(A) -> La somme de 2 chiffres est paire
-
Vérifie tes calculs pour P(A) et P(B)
-
Ddut dernière édition par
Je trouve toujours pareil pour A 12/21
par contre pour B je trouve 11/21
-
Comment trouves tu 21 ?
-
mtschoon dernière édition par mtschoon

Dut, je ne fais que passer.
Je joins un tableau à double entrée pour illustrer le nombre
d'éventualités lorsqu'on lance deux dés : 36 éventualisés6 possibilités sur le dé à chiffres noirs
A chaque valeur choisie pour le dé à chiffres noirs , il y a 6 possibilités pour le dé à chiffres bleus.
6×6=366 \times 6=366×6=36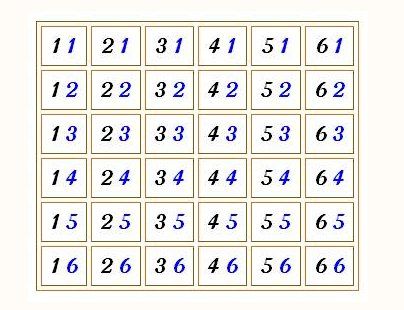
Dans chaque case, tu peux ensuite faire la somme des 2 chiffres.
Ce n'est qu' un passage. Je te laisse avec Noemi.
-
Ddut dernière édition par
(1,1) ;(1,2);(1,3);(1,4);(1,5);(1,6);(2,2);(2,3);(2,4);(2,5);(2,6);(3,3);(3,4);(3,5);(3,6);(4,4);(4,5);(4,6);(5,5);(5,6);(6,6)
Les couples possibles avec 2 dés
-
Ddut dernière édition par
Merci Mtschoon je ne différenciai pas les 2 dés car je pensais que si le premier dé vaut 1 et le second 2 c'est exactement la meme chose que si dé 1 vaut 2 etc...
-
C'est bien d'avoir compris ton erreur. Donc reprend les calculs et indique tes réponses.
-
Ddut dernière édition par
A= 19/36 et B=20/36
-
Une erreur pour P(A)P(A)P(A);
P(A)=1836=12P(A)=\dfrac{18}{36} = \dfrac{1}{2}P(A)=3618=21P(B)=2036=59P(B)=\dfrac{20}{36} = \dfrac{5}{9}P(B)=3620=95
P(A∩B)=.....P(A\cap B) = .....P(A∩B)=.....
-
Ddut dernière édition par
@Noemi a dit dans Probabilité - notion d'indépendance :
P(A∩B)=10/36
-
Oui et tu compares avec P(A)×P(B)P(A) \times P(B)P(A)×P(B) pour conclure sur l'indépendance des événements.
-
Ddut dernière édition par
0,27 = 0,5 * 0,55
0,27 = 0,27
il y a égalité donc il y a indépendance.Si il n'y avait d'égalité cela aurait dit que les événements sont dépendants?
-
Ne prends pas des valeurs arrondies mais les valeurs exactes :
P(A)×P(B)=12×59=518P(A) \times P(B) = \dfrac{1}{2} \times\dfrac{5}{9} = \dfrac{5}{18}P(A)×P(B)=21×95=185 et
P(A∩B)=1036=518P(A\cap B) = \dfrac{10}{36} = \dfrac{5}{18}P(A∩B)=3610=185
Egalité, donc les événements sont indépendants
-
Ddut dernière édition par
Merci Noemi. Donc si en faisant le calcul les valeurs ne sont pas égales alors on peut conclure que les variables ne sont pas dépendantes?
-
Oui, si tu veux dire non indépendantes.
-
Ddut dernière édition par
J'ai compris merci beaucoup
-
mtschoon dernière édition par mtschoon

@dut,
Attention !
Tu as écrit
"si en faisant le calcul les valeurs ne sont pas égales alors on peut conclure que les variables ne sont pas dépendantes?"Ce n'est pas bon.
si en faisant le calcul les valeurs ne sont pas égales alors on peut conclure que les variables ne sont pas indépendantes.
Elles sont donc dépendantes.
-
Ddut dernière édition par
Effectivement merci pour la rectification
-
mtschoon dernière édition par

De rien Dut.
Noemi a rectifié sa dernière réponse, donc maintenant, ça va.