DM maths complexes equation cercle

Bonjour, j’ai un exercice à faire sur les complexes or je bloque à la dernière question
Voici le sujet:
Le plan est rapporté au repère orthonormal (o;u;v vecteurs)
A tout point M d’affixe z=x+iy avec x,y deux reels. On associe le point M’ d’affixe $z′=5z−2z−1z'=\dfrac{5z-2}{z-1}$ pour $\ne 1$

déterminer la force algébrique de z’ en fonction de x et y
J’ai trouvé
$z′=5x2−7x+5y2−3iy+2(x−1)2+y2z'=\dfrac{5x^2-7x+5y^2-3iy+2}{(x-1)^2+y^2}$
(faute de frappe supprimée)
$X=Re(z′)=5x2−7x+5y2+2(x−1)2+y2X=Re(z')=\dfrac{5x^2-7x+5y^2+2}{(x-1)^2+y^2}$
et
$Y=im(z′)=−3y(x−1)2+y2Y=im(z')=\dfrac{-3y}{(x-1)^2+y^2}$
determiner l’ensemble (G) des points M tel que z’ est reel
J’ai donc fait im(z’)=0 et j’ai obtenu y=3

3)a) montrer que
$z+zˉ′=10zzˉ−7(z+zˉ)+4(z−1)(zˉ−1)z+\bar z'=\dfrac{10z\bar{z}-7(z+\bar{z})+4}{(z-1)(\bar{z}-1)}$

J’ai réussi à le démontrer en faisant $z+zˉz+\bar z$
3)b) en déduire que z’ est un imaginaire pur si et ssi M est point d’un cercle de centre (0,7;0) et de rayon 0,3
J’ai commencé par faire re(z’) = 0
J’ai donc repris $5x2−7x+5y2+2(x−1)2+y2=0\dfrac{5x^2-7x+5y^2+2}{(x-1)^2+y^2}=0$ soit $5x^2-7x+5y^2+2=0$
et ensuite je bloque

(Formules re-écrites en Latex par la modération)

@shana67 , bonjour,

Oui pour tes premières réponses

Une piste pour la 3)b)
L'énoncé t'indique "en déduire"
Il faut donc utiliser la 3)a)

z' imaginaire pur <=> $z′+z′‾=0z'+\overline{z'}=0$

Tu utilises la formule trouvée au 3)a)

Avec la condition dénominateur non nul, si j'ai bien lu, cela équivaut à :

$10zzˉ−7(z+zˉ)+4=010z\bar{z} -7(z+\bar z)+4=0$
Regarde les propriétés de ton cours .
Cela se traduit par :
$10(x^2+y^2)-14x+4=0$

En divisant par 10 , tu reconnais l'équation d'un cercle dont tu dois trouver centre et rayon.

Ensuite, il faut que tu vérifies que la condition "dénominateur non nul" est réalisée ou pas.

Reposte si besoin.

@mtschoon
Je ne comprend pas pourquoi on utilise cette formule la ?
Pourquoi z’ serait imaginaire pur si z’+z’barre=0

@shana67 ,

Il faut utiliser $z′+zˉ′z'+\bar z'$ pour pouvoir utiliser la question 3)a) comme demandé par l'énoncé.

Soit z'=X+iY
je t'explique pourquoi $z′+zˉ′=0z'+\bar z'=0$ équivaut à "z'imaginaire pur".
Soit :
$z^{'} = X + i Y$
$zˉ′=X−iY\bar z'=X-iY$
donc $z′+zˉ′=2Xz'+\bar z'=2X$

z' imaginaire pur <=> X=0 <=> 2X=0 <=> $\fbox{z'+\bar z'=0}$

Evidemment, si cela n'avait pas été demandé par l'énoncé, ce que tu as écrit est juste et revient exactement au même :
$5x^2-7x+5y^2+2=0$ .
En divisant par 5 tu obtiens l'expression usuelle de l'équation d'un cercle dont tu cherches centre et rayon.

$\fbox{x^2-1.4x+y^2+0.4=0}$

Pour faire apparaître centre et rayon, tu transformes

$x-0.7)^2-0.7^2+y^2+0.4=0$

$x-0.7)^2+y^2=0.09$

On peut écrire :

$\fbox{(x-0.7)^2+(y-0)^2=0.3^2}$

Tu tires la conclusion.

Bonjour,

Faute de frappe dans ta réponse 1, le "-7y" DOIT être (-7x).

Et l'énoncé est "tendancieux" pour la question 3b

Dans le cas où le point M aurait l'affixe 1 (1 + 0*i), il appartiendrait bien au cercle de centre (0,7 ; 0) et de rayon 0,3 ...
MAIS ce point ne convient pas, car pour ce point M, z' n'existe pas (on ne peut pas diviser par zéro)

@shana67 ,
J'espère que tu as tiré la conclusion à la question 3)b)
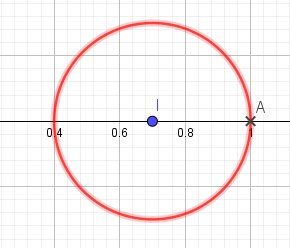
L'ensemble des points M cherché est le cercle de centre I (0,7;0) et de rayon 0,3 privé du point A(1,0)
.

@mtschoon
J’ai repris’le calcul et c’est bon la seule chose que je ne comprend pas c pourquoi on divise par 10 apres avoir factorisé ?

@shana67 ,

En repère orthonormé, la forme usuelle de l'équation d'un cercle de centre I(a,b) et de rayon R est
$\fbox{(x-a)^2+(y-b)^2=R^2}$ c'est à dire $\fbox{x^2+y^2-2ax-2by+a^2+b^2-R^2=0}$

Il est donc commode , pour une équation qui débute par $10x^2+10y^2$ de diviser par 10 pour obtenir l'équation équivalente qui débute par $x^2+y^2$ et se ramener à la forme usuelle de l'équation d'un cercle (et reconnaître le centre et le rayon du cercle).

Bon travail !

Bonjour,

Remarque déjà faite ... qui jadis aurait valu un carton rouge (mais la rigueur se perd).

"L'ensemble des points M cherché est le cercle de centre I (0,7;0) et de rayon 0,3 privé du point A."

Ah bon ? Et le point M(1 ; 0) fait partie aussi de l'ensemble cherché ???????

Bonjour @Black-Jack,

Tout à fait d'accord que l'énoncé du 3)b) est tout à fait tendancieux vu que l'on travaille non sur l'ensemble C des complexes, mais seulement sur l'ensemble C-{1} (car $z≠1z\ne 1$ c'est à dire $(x,y)≠(1,0)(x,y)\ne(1,0)$ )

Mais ce n'est pas la préoccupation de shana67 car son problème est de trouver le cercle avec centre et rayon. C'est cela qu'il faut lui expliquer le mieux possible.