3. Besoin d'aide pour 1 exercice de maths série 1er STMG

Besoin d'aide pour 1 exercice de maths série 1er STMG

  • Oasix pandaroux

    Bonjour je suis élève de 1er STMG et j'ai besoin d'aide pour mes exercices de math car je n'y arrive pas du tout (je suis très nul en math ) merci au personne qui pourront m'aider

    Sujet D
    soit f la fonction définie sur R par f(x)=−x2+5x−4f(x)=-x^2+5x-4f(x)=−x2+5x−4
    on note C la représentation graphique de f dans le plan
    1.a. Vérifier que 1 est une racine du polynôme f(x)
    b.en déduire l'écriture de f(x) sous forme factorisée
    2. Étudié les variations de la fonction f
    3. Déterminer les coordonnées des points d'intersection de C avec l'axe des abscisses
    4. Résoudre l'inéquation f(x)>0
    5. Déterminer les coordonnées exactes des points d'intersection de la courbe C et de la droite d d'équation y=-4

    Ps( j'ai mis beaucoup de temps a vous écrire ça désolée pour les fautes d'orthographe j'ai été vite et merci de bien vouloir m'aider avant ce midi s'il vous plaît merci d'avance)

    N 1 réponse
  • N
    Modérateurs

    Bonjour Oasix-pandaroux,

    Un seul exercice par post. Propose le sujet F dans un autre post.

    1 a) calcule f(1)
    b) Cherche l'autre racine de l'équation −x2+5x−4=0-x^2+5x-4 = 0−x2+5x−4=0 puis écris la forme factorisée.
    2. Calcule la dérivée de la fonction, étudie son signe et dresse le tableau de variations.
    3. Résous l'équation f(x)=0f(x)=0f(x)=0 en utilisant la forme factorisée.
    4. Fait un tableau de signes.
    5. Résous l'équation f(x)=−4f(x) = -4f(x)=−4

    Indique tes éléments de réponse si tu souhaites une correction.

    Oasix pandaroux 2 réponses
  • Oasix pandaroux

    @Noemi merci beaucoup mais je n'arive plus a posté une question

  • Oasix pandaroux

    @Noemi aussi je ne comprends pas la forme factorisée si tu pouvais m'aider ce serait vraiment gentil

    N 1 réponse
  • mtschoon

    @Oasix-pandaroux , bonjour,

    @Noemi te répondra certainement lorsqu'elle sera libre mais ces questions sont du même type que pour l'autre exercice auquel je viens de te répondre.
    Tu peux donc t'en inspirer pour répondre à celui-ci.

    Ici, f(x)=ax2+bx+cf(x)=ax^2+bx+cf(x)=ax2+bx+c avec a=−1a=-1a=−1, b=5b=5b=5 et c=−4c=-4c=−4

    Les racines sont x1=1x_1=1x1​=1 et x2=4x_2=4x2​=4 et la factorisation peut encore s'écrire f(x)=a(x−x1)(x−x2)f(x)=a(x-x_1)(x-x_2)f(x)=a(x−x1​)(x−x2​)

  • N
    Modérateurs

    @Oasix-pandaroux

    Pour la forme factorisée, vu que x=1x=1x=1 est solution, tu peux écrire :
    −x2+5x−4=(x−1)(ax+b)-x^2+5x-4 = (x-1)(ax+b)−x2+5x−4=(x−1)(ax+b)
    tu développes le terme de droite et tu détermines aaa et bbb.

  • mtschoon

    Bonjour,

    @Oasix-pandaroux a dû déjà terminé son exercice...

    Pour consultation éventuelle, pour factoriser en utilisant une seule racine (1), j'explicite la proposition de @Noemi .

    Pour tout x réel :

    (x−1)(ax+b)=−x2+5x−4(x-1)(ax+b)=-x^2+5x-4(x−1)(ax+b)=−x2+5x−4
    ax2+bx−ax−b=−x2+5x−4ax^2+bx-ax-b=-x^2+5x-4ax2+bx−ax−b=−x2+5x−4
    ax2+x(b−a)−b=−x2+5x−4ax^2+x(b-a)-b=-x^2+5x-4ax2+x(b−a)−b=−x2+5x−4

    Par identification:
    {a=−1b−a=5−b=−4\begin{cases}a=-1\cr b-a=5\cr-b=-4\end{cases}⎩⎪⎪⎨⎪⎪⎧​a=−1b−a=5−b=−4​
    c'est à dire {a=−1b=4\begin{cases} a=-1\cr b=4\end{cases}{a=−1b=4​

    Conclusion
    −x2+5x−4=(x−1)(−x+4)=−(x−1)(x−4)-x^2+5x-4=(x-1)(-x+4)=-(x-1)(x-4)−x2+5x−4=(x−1)(−x+4)=−(x−1)(x−4)

    On retrouve ainsi le résultat obtenu en cherchant d'abord les deux racines (1 et 4) et en utilisant la factorisation usuelle a(x−x1)(x−x2)a(x-x_1)(x-x_2)a(x−x1​)(x−x2​)

  • mtschoon

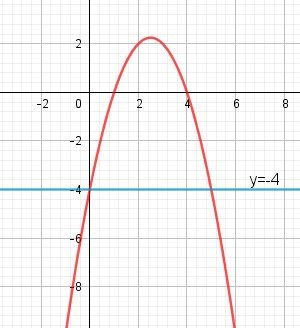
    Graphique pour pouvoir vérifier les résultats de la dernière partie
    Fonction.jpg

    Oasix pandaroux 1 réponse
  • Oasix pandaroux

    @mtschoon merci pour ce complément oui j'ai fini mais un ami étai absent ce jour donc ça pourra peut être l'aidé merci encore pour tout

  • mtschoon

    De rien @Oasix-pandaroux .
    Reviens quand tu as besoin.

Se connecter pour répondre