Devoir math cône de révolution
-
Ffanniche dernière édition par mtschoon
Soit un cône de révolution de hauteur 7,5 cm dont le rayon de base est 4 cm.
Soit S le sommet du cône, A le centre et N est un point sur le disque de base.- Calculer la longueur de la génératrice [SN].
- Calculer la valeur exacte du périmètre du disque de rayon [AN].
- Calculer la valeur exacte du périmètre du disque de rayon [SN].
- En s’aidant du tableau du cours, en déduire la valeur de l’angle du secteur circulaire, arrondir au
degré le plus proche. - Tracer le patron du cône en vraie grandeur.
-
mtschoon dernière édition par mtschoon

@fanniche , bonsoir,
Ici, il faut un peu de convivialité/politesse ...
Un petit bonjour ou bonsoir, merci, sont nécessaires .
Penses-y une autre fois si tu as besoin d'aide.Je te mets un schéma.
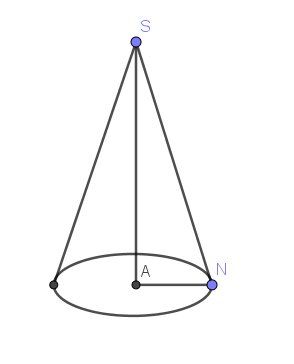
Piste pour démarrer,
1)SA=7.5SA=7.5SA=7.5
AN=4AN=4AN=4
Le triangle SAN est rectangle en A
Tu peux donc appliquer le théorème de Pythagore
SN2=SA2+AN2=(7.5)2+42SN^2=SA^2+AN^2=(7.5)^2+4^2SN2=SA2+AN2=(7.5)2+42
Tu calcules SN2SN^2SN2
Tu prends la racine carrée et tu dois trouver, sauf erreur, SN=8.5SN=8.5SN=8.5Tu poursuis.
Donne tes réponses si tu as besoin d'aide et de vérification.
-
Ffanniche dernière édition par
@mtschoon : Bonsoir,merci beaucoup pour votre aide
-
mtschoon dernière édition par mtschoon

C'est gentil @fanniche

Pour les deux questions qui suivent, tu dois calculer le périmètre d'un disque.
Je te rappelle la formule :
Peˊrimeˋtre=2×π×rayonPérimètre=2\times \pi \times rayonPeˊrimeˋtre=2×π×rayon
Tu appliques cette formule pour la 2) et pour la 3)
Reposte si tu as besoin pour la suite.
-
Ffanniche dernière édition par mtschoon
Bonjour, merci pour votre aide
Pour l'exercice 1 : j'ai fais SN² = SA²+AN²= 7.5²+4²=8.5
Pour l'exercice 2 : J'ai fais 23.144 = 25.12
Pour l'exercice 3 : J'ai fais 23.144.25 = 26.69
Pour l'exercice 4 : Je ne comprends et sais pas du tout.
Est ce que mes calculs sont corrects ? Merci d'avance pour votre aide.
-
Bonjour fanniche,
Il est demandé la valeur exacte donc :
Question 2 : périmètre du disque p=2πrp = 2\pi rp=2πr
soit p=2×π×4p = 2 \times \pi \times 4p=2×π×4 ; p=8πp = 8 \pi p=8πQuestion 3 : périmètre du disque de diamètre SN,
p=2×π×8,5p = 2 \times \pi \times 8,5p=2×π×8,5 ; p=.....πp = ..... \pi p=.....πQuestion 4 : Pour la valeur de l'angle α\alpha α en degré du secteur angulaire tu appliques la relation :
L=απr180L = \dfrac {\alpha \pi r}{180}L=180απr
-
mtschoon dernière édition par mtschoon

Pour la 2) et la 3) c'est très simple.
je t'ai donné la formule du périmètre d'un cercle.-
AN=4AN=4AN=4 donc tu calcules 2×π×42\times \pi\times 42×π×4
-
SN=8.5SN=8.5SN=8.5 donc tu calcules 2×π×8.52\times \pi\times 8.52×π×8.5
Pour la 4) tu as dû voir la méthode en cours vu que tu as un "tableau"
Si tu n'as pas compris ton cours, tu peux commencer par consulter ici :
https://www.youtube.com/watch?v=E3y1k-AG-Ok
-
-
Ffanniche dernière édition par
Bonjour et merci pour votre aide et explications.
Pour la question 2 : le résultat est 25.13 ( 2pi4)
Pour la question 3 : le résultat est 53.40 (2pi8.5)
Pour la question 4 : Je n'ai pas le cours, j'étais absent. A quoi correspond votre symbol ( α ) ? Merci.
-
mtschoon dernière édition par mtschoon

Pour les questions 2) et 3) indique les valeurs exactes
Pour la 2) 8π8\pi8π
Pour la 3 17π17\pi17πPour la 4) Vu que tu était absent en cours, comme déjà dit, commence par comprendre le cours avec la vidéo que je t'ai indiqué (pour savoir comment se fait le patron).
α\alphaα représente la valeur de l'angle du secteur angulaire
D'après ce que tu as écrit, tu dois avoir dans ton cours un tableau (j'ignore lequel) pour trouver la valeur de α\alphaα
En faisant les calculs, la valeur approchée de α\alphaα (à 0.1 près, par défaut) est 169,4°
Vu que l'énoncé te dit d'arrondir au degré le plus proche, tu dois prendre 169°Je te joins un schéma du patron, mais il faut que tu le comprennes !
Le disque bleu correspond à la base du cône
Le secteur circulaire en orange correspond à la partie latérale du cône.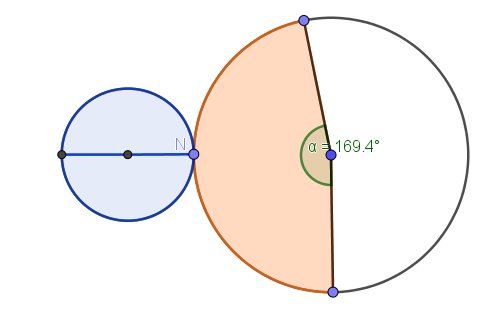
-
Ffanniche dernière édition par
Question 2 : Comment vous faites pour trouver 8 car si je fais 2×π×4, je trouve 25.13
Question 3 : Pareil, comment vous trouver 17 car si je fais 2×π×8.5, je trouve 53.40
Merci
-
mtschoon dernière édition par mtschoon

2×π×4=2×4×π=(2×4)×π=8π2\times \pi \times 4=2\times 4\times \pi=(2\times 4)\times \pi=8\pi2×π×4=2×4×π=(2×4)×π=8π
La valeur exacte est 8π8\pi8π
25,13 est la valeur approchée de 8π8\pi8π à 0.01 près (par défaut)2×π×8.5=2×8.5×π=(2×8.5)×π=17π2\times \pi \times 8.5=2\times 8.5\times \pi=(2\times 8.5)\times \pi=17\pi2×π×8.5=2×8.5×π=(2×8.5)×π=17π
La valeur exacte est 17π17\pi17π
53.40 est la valeur approchée de 17π17\pi17π à 0.01 près (par défaut)
-
Ffanniche dernière édition par mtschoon
Comment vous avez fait pour trouver 169.4 ° ? Merci
-
mtschoon dernière édition par mtschoon

Pour trouver α\alphaα tu as indiqué que tu avais un tableau
Comme on ne l'a pas, on ne peut pas te dire comme tu dois faire avec ce tableau....Je peux t'indiquer un raisonnement qui te permet d'obtenir α\alphaα ( mais utilise la méthode de ton cours avec le "tableau" qui doit éviter ces calculs )
Pour le patron de la surface latérale du disque :
Pour un angle au centre de 360°, le périmètre du cercle est 17π17\pi17π
Pour un angle au centre de α\alphaα°, l'arc de cercle a une longueur de 8π8\pi8πTu obtiens la proportion α360=8π17π\dfrac{\alpha}{360}=\dfrac{8\pi}{17\pi}360α=17π8π
En simplifiant par π\piπ
α360=817\dfrac{\alpha}{360}=\dfrac{8}{17}360α=178d'où
α=8×36017\alpha=\dfrac{8\times 360}{17}α=178×360
-
Ffanniche dernière édition par
Merci beaucoup pour toutes vos explications et patience. Bonne après-midi.
-
mtschoon dernière édition par

De rien @fanniche .
Essaie de voir de près le cours qui t'a manqué et refais seul l'exercice pour être sûr de le maîtriser.
-
Ffanniche dernière édition par
Merci pour votre conseil que je vais appliqué. Encore merci.
-
mtschoon dernière édition par

Bon travail @fanniche