polynôme et loi uniforme

Bonjour,
j'ai un polynôme quelconque x²+bx+c
J'aimerais trouvé la probabilité que ce polynôme est 1 seule racine donc que son lambda soit = à 0.
En sachant qu'on ne tire (indép et unif dans [0,1]) b et c.
je pense que l'intervalle contient 11 valeurs: 0; 0.1; 0.2; 0.3; 0.4;...; 1
Pour que lambda soit = à 0 il faut que b et c valent 0
Donc il y a une combinaison possible sur 22 (2 tirages indep = 112)

Cela vous parait juste?
Merci

Bonjour cours ,

$Δ=b2−4ac\Delta =b^2-4ac$ , vu que $a = 1$ ,
$Δ=b2−4c\Delta =b^2-4c$ soit $b^2 = 4c$ .

Bonjour et merci
Il n'y a donc bien qu'une seule possibilité? Le cas b et c = 0?
Est ce que uniformément veut bien dire : 0, 0.1, ....,1 soit 11 valeurs possibles?
La réponse est donc 1/22

@cours

Il n'y a pas une seule solution, par exemple $b = 0, 2$ et $c = 0, 01$ .

effectivement mais comment je peux savoir le nombre de valeur contenues dans l'intervalle [0,1]?

@cours

Cela dépend des valeurs de l'intervalle, la précision.

Cette question fait-elle suite à une autre question ?

Pas du tout c'est une question "isolée".
Il y a une infinité de possibilité dans l’intervalle ça va être compliqué de trouver une probabilité

@cours

Quelle est la précision sur l'intervalle [0 ; 1 ] ?

@Noemi et @cours , bonjour,

@cours ,
Je me permets de te donner une version pour le cas où les variables b et c sont des variables uniformes continues sur [0,1] et indépendantes.
Si c'est le cas, le couple (b,c) prend les valeurs dans $[0,1]×[0,1][0,1]\times[0,1]$ représenté par le carré en vert dans le schéma joint.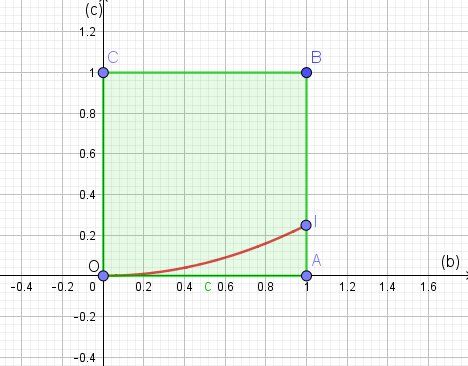

Comme indiqué par @Noemi, avoir une seule solution correspond à $b^2=4c$ c'est à dire $c=14b2c=\frac{1}{4}b^2$
Cela est représenté sur le schéma par la portion de parabole en rouge.
La probabilité cherchée est nulle vu qu'il s'agit d'une "courbe d'épaisseur nulle"

Remarque :
Si on avait cherché la probabilité pour que l'équation ait 2 racines distinctes :
$Δ>0\Delta \gt 0$ <=> $c<b24c\lt \dfrac{b^2}{4}$

La probabilité serait l'aire de la zone sous la courbe en rouge.
En faisant le calcul intégral, on trouverait
$∫01b24db=14[b33]01=112\displaystyle \int_0^1\dfrac{b^2}{4}db=\dfrac{1}{4}\biggr[\dfrac{b^3}{3}\biggr]_0^1=\dfrac{1}{12}$

Si on avait cherché la probabilité pour que l'équation n'ait aucune racine, on aurait trouvé comme probabilité $1−112=11121-\dfrac{1}{12}=\dfrac{11}{12}$

Autre remarque :
Comme indiqué, cela s'applique exclusivement dans les cas de variables continues sur [0,1] et indépendantes.

S'il s'agit de variables discrètes sur [0,1] et indépendantes, le problème est autre, mais dans ce cas l'énoncé est incomplet....(et je rejoins la dernière question posée par Noemi et à laquelle il faudra que tu répondes en donnant des précisions, pour pouvoir faire le calcul)

Bonsoir et merci pour ces réponses.

Quelle est la méthode pour arriver à tracer la parabole rouge?
Je ne comprends pas "l'épaisseur nulle"
Pourquoi où dans le cas où on cherche 2 racines distinctes c doit être < b²/4 ?

Merci par avance

cours

@cours ,

Je regarde tes 3 questions.

La parabole rouge a pour équation
$c=14b2\boxed{c=\dfrac{1}{4}b^2}$ pour b compris entre 0 et 1
(elle correspond au cas $Δ=0\Delta=0$ )

b représente l'abscisse (appelé x habituellement)
c représente l'ordonnée ( appelée y habituellement)
En bref, pense que c'est $y=14x2\boxed{y=\dfrac{1}{4}x^2}$
Vu qu'il s'agit d'une fonction polynôme du second degré, la représentation graphique est une portion de parabole
Pour la représenter, prends quelques points
Pour x=0, y=0
Pour x=1/4, y=1/64
Pour x=1/2, y=...
Pour x=3/4, y=...
Pour x=1, y=1/4

Mathématiquement parlant, tout point est de dimension nulle (pense qu'un point est" infiniment petit") .
Pour "l'épaisseur nulle", tu peux imaginer "trait infiniment mince"
Deux racines distinctes correspond à $Δ>0\Delta \gt 0$

$b2−4c>0b^2-4c \gt 0$ <=> $\gt -b^2$ <=> $\lt b^2$ <=> $c<14b2\boxed{c\lt \dfrac{1}{4}b^2}$

j'espère avoir répondu à tes questions.

Bonjour
merci pour l'explication et désolé pour la réponse tardive.
J'ai bien compris l'intégration et les différents calculs.
Mais en relisant je ne comprends pas pourquoi le 'a' du delta est mis à 1.
Initialement je pensais que ça correspondait à 1 seule racine mais dans le cas ou delta est supérieur à 0 le a est aussi = à 1 vu qu'il n’apparaît pas dans le calcul

Comment sais t'on que b représente l'abscisse et c l'ordonnée?

@cours

L'équation proposée dans l'énoncé est : $x^2+bx+c= 0$
Pas de $a$ devant $x^2$ donc on peut écrire $a = 1$

Pour la fonction, vu que tu représentes $c$ en fonction de $b$ ,
$b$ est en abscisse et $c$ en ordonnée.

Merci j'ai compris

Par curiosité comment faudrait-il faire dans le cas où a >1 donc avoir a,b et c?

@cours , bonjour,

Désolée d'avoir mis plusieurs jours à te répondre.
(J'ai été absente...famille oblige ! )

Dans ce cas, $Δ=0\Delta=0$ correspond à $c=b24ac=\dfrac{b^2}{4a}$

Si tu fais une interprétation graphique, dans l'esprit de la réponse précédente, tu trouves une surface (S) en dimension 3, dans une repère de l'espace.
Probabilité nulle comme précédemment.

$Δ>0\Delta \gt 0$ correspond à $c<b24ac\lt\dfrac{b^2}{4a}$

Ceci correspond au calcul du volume de la zone en dessous de (S) (et dans la portion d'espace délimitée par $a>1a\gt 1$ , $0≤b≤10\le b\le 1$ et $0≤c≤10\le c\le 1$

Pour cela, un calcul d'une intégrale multiple est nécessaire (au lieu d'une intégrale simple comme dans la question de départ).
On est alors très très loin du programme de Terminale...

Ne te fais pas de soucis, tu ne risque pas d'avoir une telle question au bac (car tout à fait hors programme...).

Bon travail ( et bonne année 2020).

Merci pour l'aide

De rien @cours ,
Reviens si tu as besoin, une autre fois.