Fonction exponentielle montrer qu elle est croissante

[margotguerinc]

Bonjour , je dois faire un DM , sur le chapitre des fonctions exponentielles.
Je suis bloquée à la dérivation de :
f(x)= 0,01xe^x - 0.01 e^x - 2
car si on dérive bah sa fait 0 mais après il faut montrer que f est strictement croissante sur l’intervalle [0;6] et je comprends rien

[mtschoon]

@margotguerinc , bonjour,

si f(x) est bien $\fbox{f(x)=0.01xe^x-0.01e^x-2}$,
pour f'(x) tu dois trouver
$\fbox{f'(x)=0.01xe^x}$

Pour x=0, f'(x)=0
pour x > 0, vu que $e^x>0$, f'(x) >0 donc .........(tu termines)

Est-ce bien ce que tu as trouvé?

Reposte si ce n'est pas le cas.

[margotguerinc]

@mtschoon , bonjour , merci pour votre réponse ,

Et bien mon soucis c’était la dérivation de f(x) , car je comprend pas comment vous avez trouvé f’(x) = 0,01xe^x , fin pour moi quand on dérive f(x) c’est :

f(x)=0.01xe^x - 0,01e^x -2
f'(x)=0,01e^x - 0.01e^x
f'(x)= 0
comment on fait il faut factoriser ?

[Noemi]

Bonjour margotguerinc,

Le premier terme de $f(x)$ est de la forme $U\times V$, avec $U=0,01x$ et $V=e^x$
sa dérivée est $U^{\prime }V+U{V}^{\prime }$
Il manque dans ton calcul $U{V}^{\prime }$ soit $0,01x{e}^x$.

[margotguerinc]

@Noemi , aaah okkk merci bcp , j’avais pas du tout vu c’est un piège faut que je fasse attention merci beaucoupp !

[mtschoon]

@margotguerinc , bonsoir,

Effectivement, tu as fait une erreur sur la dérivée d'un produit.
Noemi te l'a rectifiée.
Maintenant, tu as compris , c'est l'essentiel.

Avec ton erreur, tu trouvais f'(x)=0 . Cela aurait prouvé que f était constante, ce qui n'est pas le cas.

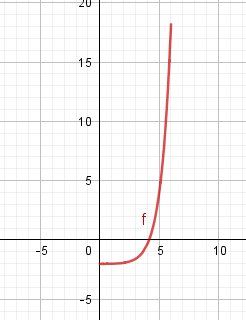
Pour illustration, je te joins le graphique de f pour $x\in [0,6]$