cylindre inscrit dans une sphère
-
Aariel dernière édition par
Dans une sphère de rayon R ,on inscrit un cylindre de hauteur h .
Les deux bases du cylindre sont des cercles de la sphère de rayon r.Pour quelle valeur de h le volume est-il maximal?
-
Aariel dernière édition par
pouvez-vous m'aidez svp?
-
Bonjour ariel, (Marque de politesse à ne pas oublier !!)
Je suppose que l'on cherche le volume maximal du cylindre.
Il faut exprimer le volume en fonction de la hauteur hhh.
Comme : V=πr2hV = \pi r^2hV=πr2h.
Il reste à exprimer rrr en fonction de hhh et RRR.
Un schéma et la propriété de Pythagore.
-
Aariel dernière édition par
c'est ca la formule?
-
Aariel dernière édition par
quelqu'un pour m'aider s'il vous plait
-
mtschoon dernière édition par mtschoon

@ariel , bonsoir,
Je te joins une figure en coupe.
Le disque correspond au cercle de centre A de de rayon R
Le cylindre correspond au rectangle BCDE
L'axe du cylindre est (FG)
A est le milieu de [FG]
EF=r
EA=R
AF=h/2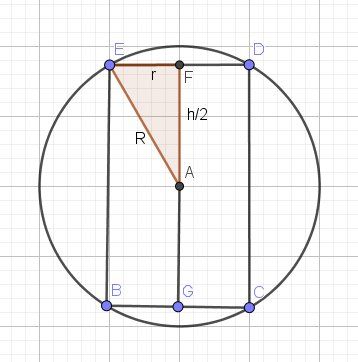
Piste pour démarrer,Applique le théorème de Pythagore dans le triangle AEF rectangle en F
EA²=EF²+FA²
R2=r2+(h2)2R^2=r^2+(\dfrac{h}{2})^2R2=r2+(2h)2
-
Dans la formule du volume en utilisant la relation donnée par mtschoon tu remplaces r2r^2r2 par son expression en fonction de hhh et RRR.
Tu cherches ensuite la valeur de hhh qui correspond au maximum de la fonction.
-
Aariel dernière édition par
comment faire cela ?
-
Commence par écrire l'expression du volume en fonction de hhh et RRR :
V=......V = ......V=......
-
Aariel dernière édition par
V= piR^2h Mais je cherches le volume maximal
-
Je n'ai pas écrit de faire un calcul mais juste d'écrire l'expression :
V=πr2hV = \pi r^2 hV=πr2h et tu remplaces r2r^2r2 par R2−(h2)2R^2 - (\dfrac{h}{2})^2R2−(2h)2
Soit V=.....V = .....V=.....
-
Aariel dernière édition par
V=piR^2-(h/2)^2h c'est bon?
-
Il manque des parenthèses.
V=π(R2−(h22))hV = \pi (R^2 -(\dfrac{h}{2}^2))hV=π(R2−(2h2))h
-
Aariel dernière édition par
ok et après je fait quoi ?
-
Tu étudies cette fonction pour déterminer son maximum.
Comment étudies tu les variations d'une fonction ?
Calcul de la dérivée ou taux de variation ?
-
Aariel dernière édition par
comment étudie-t'on le maximum?
-
Cherche les variations de la fonction.
-
Aariel dernière édition par
je vais essayer de calculer la dérivée:
V= 2piR-2(h/2)*2 c'est bon
-
@ariel
Non
V′(h)=πR2−π×34h2V'(h) = \pi R^2 - \pi \times \dfrac{3}{4}h^2V′(h)=πR2−π×43h2Résous V′(h)=0V'(h) = 0V′(h)=0.
-
Aariel dernière édition par
Tu peux m'expliquer comment t'a abouti a ce résultat?
-
V(h)=π(R2−(h22))hV(h) = \pi (R^2 -(\dfrac{h}{2}^2))hV(h)=π(R2−(2h2))h. On développe
V(h)=πR2h−πh43V(h) = \pi R^2h - \pi \dfrac{h}{4}^3V(h)=πR2h−π4h3
et tu dérives chaque termes, la variable est hhh.
-
Aariel dernière édition par
ok merci après cela quesceque je fais?
-
Tu résous V′(h)=0V'(h)= 0V′(h)=0.
Puis tu étudies le signe de la dérivée et tu dresses le tableau de variations.
-
Aariel dernière édition par
pourquoi V'(h)= piR^2-pi3/4h^2
-
mtschoon dernière édition par mtschoon

@ariel ,
Si c'est le calcul de la dérivée qui te pose problème,V(h)=πR2h−π4h3V(h)=\pi R^2h-\dfrac{\pi}{4}h^3V(h)=πR2h−4πh3
h est la variable.
Dans ton cours, j'imagine que la variable s'appelle x
Pense donc que h=x, c'est à dire que
V(x)=πR2x−π4x3V(x)=\pi R^2x-\dfrac{\pi}{4}x^3V(x)=πR2x−4πx3πR2\pi R^2πR2 joue le rôle de constante vu que la variable est x
La dérivée de x est 1
Regarde ton cours sur les propriétés : la dérivée deπR2x\pi R^2 xπR2x est donc πR2×1=πR2\pi R^2 \times 1=\pi R^2πR2×1=πR2De même, π4\dfrac{\pi}{4}4π joue le rôle de constante vu que la variable est x
La dérivée de x3x^3x3 est 3x23x^23x2
Donc la dérivée de π4x3\dfrac{\pi}{4}x^34πx3 est π4×3x2\dfrac{\pi}{4} \times 3x^24π×3x2La dérivée d'une différence est la différence des dérivées
V′(x)=πR2−3π4x2V'(x)=\pi R^2-\dfrac{3\pi}{4}x^2V′(x)=πR2−43πx2
J'ai utilisé la notation x usuelle pour te faire comprendre, mais ton exercice, utilise seulement la notation h
V′(h)=πR2−3π4h2\boxed{V'(h)=\pi R^2-\dfrac{3\pi}{4}h^2}V′(h)=πR2−43πh2
C'est ce que t'a indiqué Noemi.
-
A partir de la dérivée, tu détermines son signe puis le tableau de variations comme fait dans l'autre exercice.
-
Aariel dernière édition par
mais comment étudier le signe avec un résultat pareil?-_-'
-
Tu résous d'abord V′(h)=0V'(h) = 0V′(h)=0.
-
Aariel dernière édition par
piR^2-pi3/4h^2=0
R^2-3*pi/4h^2=pi
-
Aariel dernière édition par
merci pour tout Noémie bonne nuit
-
V′(h)=πR2−π3h24V'(h) = \pi R^2- \pi \dfrac {3h^2}{4}V′(h)=πR2−π43h2
V′(h)=0V'(h) = 0V′(h)=0 si πR2−π3h24=0\pi R^2- \pi \dfrac {3h^2}{4} = 0πR2−π43h2=0Soit R2−3h24=0R^2- \dfrac {3h^2}{4} = 0R2−43h2=0
On isole l'inconnue hhh
h2=4R23h^2 = \dfrac {4R^2}{3}h2=34R2
soit h=233Rh = \dfrac {2\sqrt3}{3} Rh=323R ou h=−233Rh =- \dfrac {2\sqrt3}{3} Rh=−323R
Comme hhh positif, je te laisse conclure.
Ne pas oublier de préciser les variations de la fonction.
-
Maxime THIERRY dernière édition par
Bonjour @Noemi , y a t'il possibilité d'avoir une explication pour le tableau de variation ?
-
Maxime THIERRY dernière édition par
ou alors de votre part @mtschoon
-
mtschoon dernière édition par mtschoon

@Maxime-THIERRY , bonsoir,
Pour h≥0h\ge 0h≥0,tu dois étudier le signe de V'(h)
De plus, h≤2Rh\le 2Rh≤2R pour que la construction soit possible.Vu que h est positif, vu le calcul effectué précédemment ,
V′(h)=0V'(h)=0V′(h)=0 pour h=233Rh=\dfrac{2\sqrt 3}{3}Rh=323RIl te reste à chercher pour quelles valeurs de h V'(h) est strictement positif, puis strictement négatif.
V′(h)>0V'(h) \gt 0V′(h)>0 <=> πR2−3π4h2>0\pi R^2-\dfrac{3\pi}{4}h^2\gt 0πR2−43πh2>0
−3π4h2>−πR2-\dfrac{3\pi}{4}h^2 \gt -\pi R^2−43πh2>−πR2
En changeant de signe pour éviter les erreurs (c'est à dire en multipliant par -1)
3π4h2<πR2\dfrac{3\pi}{4}h^2 \lt \pi R^243πh2<πR2Tu isoles h2h^2h2 et tu dois trouver h2<43R2h^2\lt \dfrac{4}{3}R^2h2<34R2
Vu que h est positif, en prenant la racine carrée de chaque membre : h<233Rh\lt \dfrac{2\sqrt 3}{3}Rh<323RDonc : 0≤h<233R0\le h\lt \dfrac{2\sqrt 3}{3}R0≤h<323R <=> V′(h)>0V'(h)\gt 0V′(h)>0 donc V croissante.
De même : h>233Rh\gt \dfrac{2\sqrt 3}{3}Rh>323R <=> V′(h)<0V'(h)\lt 0V′(h)<0 donc V décroissante.
Tu peux donc faire le tableau de variation pour h∈[0,2R]h\in [0,2R]h∈[0,2R] et tirer la conclusion demandée.
-
Maxime THIERRY dernière édition par Maxime THIERRY
-
mtschoon dernière édition par

-
Maxime THIERRY dernière édition par
@mtschoon pouvez vous me montrez en expliquant ?
-
mtschoon dernière édition par

Relis avec soin ma réponse où je t'explique le signe de V'(h) et le sens de variation de V.
-
Maxime THIERRY dernière édition par
@mtschoon je n'arrive pas à le représenter dans un tableau de variation
-
Maxime THIERRY dernière édition par
@mtschoon pouvez vous le faire et qu'on regarde ensemble ?
-
mtschoon dernière édition par mtschoon

Je recopie ce que je t'ai déjà indiqué :
0≤h<233R0\le h\lt \dfrac{2\sqrt 3}{3}R0≤h<323R <=> V′(h)>0V'(h)\gt 0V′(h)>0 donc V croissante.
De même : h>233Rh\gt \dfrac{2\sqrt 3}{3}Rh>323R <=> V′(h)<0V'(h)\lt 0V′(h)<0 donc V décroissante.
cela veut dire que :
Pour h compris entre 0 et 233\dfrac{2\sqrt 3}{3}323, V'(h) est positive ( signe +) et V est croissante (flèche qui monte)
Pour h compris entre 233\dfrac{2\sqrt 3}{3}323 et 2R2R2R , V'(h) est négative ( signe - ) et V est décroissante (flèche qui descent)
Il y a donc un maximum pour h=...
-
Maxime THIERRY dernière édition par
@mtschoon (2 racine carré de 3)/3 ?
-
mtschoon dernière édition par

J'espère que tu as bien compris les erreurs que tu avais faites sur le tableau de variation joint et que tu les as rectifiées.
Oui, le maximum est bien pour h=233h=\dfrac{2\sqrt 3}{3}h=323
-
mtschoon dernière édition par mtschoon

Je te mets le tableau de variation pour vérification éventuelle.
Je te conseille d'approfondir toute la discussion vu que tu n'as posé ta question que sur la fin de la démarche.
Il faut que tu comprennes la totalité.Dans le tableau de variation, ce que j'ai appelé MAX est V(233)V(\dfrac{2\sqrt 3}{3})V(323)
Dans l'énoncé écrit, le calcul de cette valeur n'est pas demandé.

Bon travail.