Algorithme newton-Raphson

bonsoir pouvez-vous m'aidez svp?

PARTIE A:
Soit Xn+1 l'abscisse du point d'intersection de la tangente (Tn) à Cf en Xn avec l'axe des abscisses.
1)déterminer l'équation de la tangente en Xn
2)montrer alors que l'on a : Xn+1=Xn-f(Xn)/f'(Xn)
3)quelles conditions doit vérifier f pour que la suite (Xn) existe sur N?
on suppose dans la suite que cette condition est vérifiée.

PARTIE B:
Le but est de trouver une approximation à 10^-3 près de la solution de : x^3-2x-5=0
soit la fonction f définie sur R par: f(x)=x^3-2x-5
1)Déterminer les variations de la fonction f sur l'intervalle R puis montrer que l'équation f(x)=0 admet une unique solution alpha dans [2;3]

soit la suite (Xn) définie sur N par x0=2 et Xn+1=Xn-f(Xn)/f'(Xn)
on admet que la suite (Xn)converge vers alpha.
a) remplir le tableau suivant :

n Xn f(Xn) f'(Xn) -f(Xn)/f'(Xn) Xn+1

b) si l'on prend comme critère d’arrêt [f(Xn)/f'(Xn)]inférieur ou p correspond à la précision ,quelle -est la précision de alpha obtenue par ce tableau?
c)que peut on dire de la performance de cet algorithme ?
PARTIE
on recherche un nombre x vérifiant cosx=x. on pose alors f(x)=cos x-x

1)calculer la fonction dérivée f' puis montrer que l'équation cos x=x admet une solution alpha dans l'intervalle [0;1]
2) écrire un programme permettant de déterminer alpha à 10^-6 près et le nombre de boucles nécessaires

on prendra comme critère[f(Xn)/f'(Xn)]inférieur à p ou p correspond à la précision .

Faire fonctionner ce programme pour trouver alpha à 10^-6
svp aidez moi je ne comprends rien du tout

Bonjour @ariel,

Tu as déjà posé le début de cet exercice dans un autre post. Il faudrait continuer sur le premier post. J'ai répondu déjà au deux premières questions.

Pour rappel, le multiposts est interdit sur ce forum.

Il est important que tu indiques tes calculs et recherche si tu souhaites une aide ou correction.

bonjour,
je souhaite une correction et comprendre le processus

peut tu m'aider pour les autres questions , le premier exercice sur l'algorithme n'est pas complet désolée?

@ariel

Tu aurais du écrire la suite de l'énoncé sur ton premier post.

Pour la partie B :
Indique tes résultats ou calculs et la question qui te pose problème.

Calcul de la dérivée, signe de la dérivée puis variations de la fonction, théorème des valeurs intermédiaires.

comment déterminer les variations ?

@ariel

Suis les indications données dans mon précédent post.

ok mais d'abord je dérive la fonction?

@ariel

Oui
Calcule $f^{'} (x) = . . . .$

f'(x)=3x^2-2 et après?

Tu résous $f^{'} (x) = 0$ puis tu étudies le signe de $f^{'} (x)$ pour en déduire les variations.

3x^2-2=0
3x^2=2
x^2=2/3
x=4/9 c'est bon?

Non,
$x2=23x^2 = \dfrac{2}{3}$ admet comme solutions $\sqrt\dfrac{2}{3}$ et $-\sqrt\dfrac{2}{3}$
que l'on peut écrire $\dfrac{\sqrt6} {3}$ et $-\dfrac{\sqrt6} {3}$

Etudie le signe de la dérivée.

il faut faire un tableau?

x -infini -racine carré de 2/3 racine carré de 2/3 +infini
f'(x) + - +
f(x) croissant décroissant croissant

c'est bon ou pas?

c'est pas x1 et x2?

Tu peux écrire $x_1$ et $x_2$ en précisant leur valeur.
Le tableau de variations est juste. Il faudrait préciser les valeurs extrêmes des flèches.

je ne peux faire des flèches ,il faut faire cela sur l'intervalle [2;3]?

comment faire? tu me dit mon tableau est juste , l'intervalle quescequ'on en fait?

Le tableau de variations est juste mais il faut indiquer pour la question suivante que sur l'intervalle $[63;+∞[[\dfrac{\sqrt6}{3} ; +\infty[$ la fonction est continue est croissante. L'intervalle [2; 3] appartient à l'intervalle $[63;+∞[[\dfrac{\sqrt6}{3} ; +\infty[$ . De plus $f (2) = . . .$ et $f (3) = . . . . .$
donc il existe un $α\alpha$ tel que $f(α)=0f(\alpha)= 0$ d'après le théorème des valeurs intermédiaires.

donc je ne change rien a mon tableau? je marque juste à la question suivante l'intervalle ? ok merci

Pour le tableau de la question 2,
$x_0 = 2$
$n = 0, x_0 = 2, f(2) = ... , f'(2) = ....$
$n = 1, x_1 = ...., .....$

A compléter

je vais essayer f(2)=-1, f'(2)=il faut faire le taux d'accroissement? je n'y comprends plus rien?

Pour $f^{'} (x)$ , utilise la dérivée : $f'(x)=3x^2 - 2$ .

n Xn f(Xn) f'(Xn) -f(Xn)/f'(Xn) Xn+1

n et juste en dessus 3carreau; f(Xn);f'(Xn)........

Complète l'avant dernier message.

je sais pas comment le remplir mais je vais essayer

f(2)=-1

c'est bon? mais les autres je n'arrive pas

Sais tu utiliser un tableur ?
Pour $n = 0$
$f'(x) = 3x^2 - 2$ ; $3\times 4 - 2 = 10$
$−f(x0)f′(x0)=−−110=0,1-\dfrac{f(x_0)}{f'(x_0)}= -\dfrac{-1}{10} = 0,1$

$x_1=2 +0,1 = 2,1$

Tu appliques le même raisonnement pour $n = 1$ soit avec $x_1 =2,1$ .

merci beaucoup

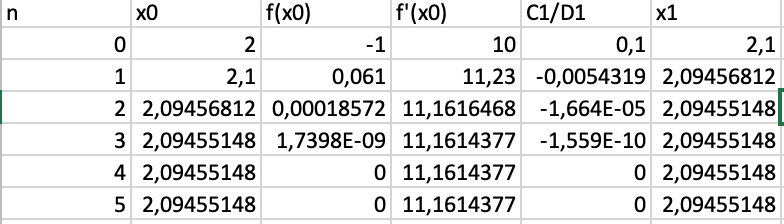
Voici ce que tu devrais obtenir avec un tableur :

c'est super dur? tu pourras m'expliquer?

Il suffit de savoir utiliser un tableur, soit écrire les formules.