continuité et partie entière
-
Mmathematiques123 dernière édition par
bonjour , j'arrive pas à étudier la continuité d'une fonction avec partie entière .
voici mon énoncé :
Etudier la continuité de la fonction f définie sur [0;+linfini[ par :
f(x)=E(x/x+1)
E désigne la fonction partie entière
Aidez moi s'il vous plaît
et merci
-
mtschoon dernière édition par mtschoon

@mathematiques123 , bonjour
Si j'ai bien lu,
f(x)=E(xx+1)f(x)=E\biggl(\dfrac{x}{x+1}\biggl)f(x)=E(x+1x)Pour x≥0x\ge 0x≥0 , tu peux écrire 0≤x<x+10\le x\lt x+10≤x<x+1
En divisant par (x+1) qui est strictement positif, tu obtiens
0x+1≤xx+1<x+1x+1\dfrac{0}{x+1}\le \dfrac{x}{x+1}\lt \dfrac{x+1}{x+1}x+10≤x+1x<x+1x+1, c'est à dire$\fbox{0\le \dfrac{x}{x+1}\lt 1}$
La partie entière de tout nombre de l'intervalle [0,1[ vaut 0, donc
E(xx+1)=0E\biggl(\dfrac{x}{x+1}\biggl)=0E(x+1x)=0La fonction f est donc la fonction nulle pour x∈[0,+∞[x \in [0,+\infty[x∈[0,+∞[, donc forcémnent continue.
-
mtschoon dernière édition par

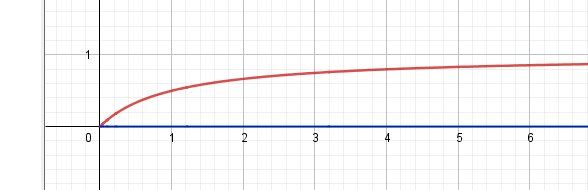
Illustration graphique
La fonction g définie par g(x)=xx+1g(x)=\dfrac{x}{x+1}g(x)=x+1x est en rouge
La fonction f définie par f(x)=E(xx+1)f(x)=E\bigg(\dfrac{x}{x+1}\biggl)f(x)=E(x+1x) est en bleu