les équations trigonométriques

Bonjour, j'ai un devoir maison de mathématiques à faire pour demain et je bloque sur deux exercices, voici le second:
Résoudre les équations trigonométriques suivantes :

pour tout x appartenant au réel sin(2x - pi/3)-sin((3x+pi/2) = 0
pour tout x appartenant ]-pi;pi[ cos(x+ pi/4) = sin(3x)
Remarque on pourra utiliser la propriété : 2x = teta[2pi] <-> x = (teta/2)[pi].

@leo04 , bonjour,

Je te mets des relations utiles,

En transposant un terme d'un membre dans l'autre, tu obtiens une égalité de la forme $s i n a = s i n b$

$s i n a = s i n b$ <=> $a=b+2kπa=b+2k\pi$ ou $a=π−b+2kπa=\pi-b+2k\pi$ avec $k∈Zk\in Z$

Cela peut s'écrire :
$s i n a = s i n b$ <=> $[2π]a=b\ [2\pi]$ ou $[2π]a=\pi-b\ [2\pi]$

Tu résous.

Tu peux transformer cos en sin avec l'égalité $cosa=sin(π2−a)cosa=sin(\frac{\pi}{2}-a)$

Ensuite, tu utilises la même propriété qu'au 1. puis tu résous.

Tiens nous au courant de tes avancées si tu as besoin.

Bonjour,

Pour vérification éventuelle,

Sauf erreur, on trouve :

$[2π]\ x=\dfrac{-5\pi}{6}\ [2\pi]$ ou $[2π5]x=\dfrac{\pi}{6}\ [\dfrac{2\pi}{5}]$
Après avoir transformer l'équation en
$sin(π4−x)=sin3xsin(\dfrac{\pi}{4}-x)=sin3x$

$[π2]\ x=\dfrac{\pi}{16}\ [\dfrac{\pi}{2}]$ ou $[π]x=\dfrac{3\pi}{8}\ [\pi]$

Restreindre les solutions à $]−π,π[]-\pi,\pi[$

A vérifier, bien sûr.

Bonjour je viens de m'y remettre avec mon cours à côté mais c'est un chapitre avec lequel j'ai beaucoup de mal, je bloque toujours...

@leo04 Re-bonjour,

Je te détaille les calculs de la question 1), mais bien sûr, il faut maîtriser le cours pour comprendre.
Si ça peut t'aider, je te mets un schéma

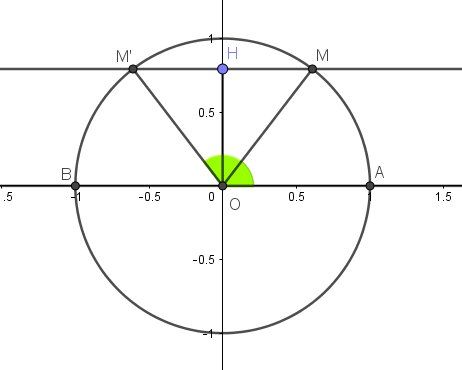
Sur le cercle trigonométrique, les angles $(OA→,OM→)(\overrightarrow{OA},\overrightarrow{OM})$ et $(OA→,OM′→)(\overrightarrow{OA},\overrightarrow{OM'})$ sont les angles ayant pour sinus la mesure algébrique $OH‾\overline{OH}$
C'est angles sont supplémentaires : à $2π2\pi$ près, l'un vaut $a$ , l'autre vaut $π−a\pi-a$

Lorsque deux angles ont même sinus, ils sont soit égaux soit supplémentaires.

$s i n a = s i n b$ <=> $a=b+2kπa=b+2k\pi$ ou $a=π−b+2kπa=\pi-b+2k\pi$ avec $k∈Zk\in Z$

Merci mais comment résoudre ensuite ?

Dans la question 1)
$a=2x−π3a=2x-\dfrac{\pi}{3}$ et $b=3x+π2b=3x+\dfrac{\pi}{2}$

1er cas : $a=b+2kπa=b+2k\pi$
$2x−π3=3x+π2+2kπ2x-\dfrac{\pi}{3}=3x+\dfrac{\pi}{2}+2k\pi$
En transposant
$2x−3x=π3+π2+2kπ2x-3x=\dfrac{\pi}{3}+\dfrac{\pi}{2}+2k\pi$
Après calculs
$−x=5π6+2kπ-x=\dfrac{5\pi}{6}+2k\pi$
En multipliant par -1
$x=−5π6−2kπx=\dfrac{-5\pi}{6}-2k\pi$
Vu que k est un entier quelconque (positif ou négatif), on peut écrire
$x=−5π6+2kπ\boxed{x=\dfrac{-5\pi}{6}+2k\pi}$

2ème cas : $a=π−b+2kπa=\pi-b+2k\pi$
$2x−π3=π−(3x+π2)+2kπ2x-\dfrac{\pi}{3}=\pi-(3x+\dfrac{\pi}{2})+2k\pi$
$2x−π3=π−3x−π2−2kπ2x-\dfrac{\pi}{3}=\pi-3x-\dfrac{\pi}{2}-2k\pi$
En transposant
$2x+3x=π−π2+π3+2kπ2x+3x=\pi-\dfrac{\pi}{2}+\dfrac{\pi}{3}+2k\pi$
Après calculs
$5x=5π6+2kπ5x=\dfrac{5\pi}{6}+2k\pi$
En divisant par 5
$x=π6+2kπ5\boxed{x=\dfrac{\pi}{6}+\dfrac{2k\pi}{5}}$

Lorsque tu auras compris, essaie de faire la question 2) avec les pistes indiquées et reposte si besoin

ok j'ai tout compris merci.
Je tente et vous recontacte d'ici 10mn.

Sachant que cosx = sin(pi/2-x) alors cos(x+pi/4) = sin(pi/2-x-pi/4) est-ce bien cela ?

si oui comment faire la suite ?

@leo04 ,

Ce que tu as écrit est exact.
Vu que $π2−π4=π4\dfrac{\pi}{2}-\dfrac{\pi}{4}=\dfrac{\pi}{4}$ , l'équation se ramène à :
$sin(π4−x)=sin(3x)\boxed{sin(\dfrac{\pi}{4}-x)=sin(3x)}$

Tu appliques la méthode vu : sina=sinb <=>....
Tu fais les deux cas.
Tu obtiendras toutes les solutions réelles et il faudra ensuite restreindre à $]−π,π[]-\pi,\pi[$

j'ai trouvé c'est bon ! j'obtiens maintenant pi/16

@leo04
Oui, dans le premier cas $x=π16+kπ2x=\dfrac{\pi}{16}+\dfrac{k\pi}{2}$

et le deuxième 3pi/8 + kpi, c'est bon ?

les solutions dans l'intervalle sont donc pi/16 + 2pi/2 et pi/16 + 4pi/2 et 3pi/8 +pi et 3pi/8 +2pi ?

Vérifie tranquillement les valeurs de k.
Elles ne sont pas toutes bonnes.

@leo04,

Oui, pour le second cas, tu dois trouver $x=3π8+kπx=\dfrac{3\pi}{8}+k\pi$

oui j'avais compris cela mais je ne vois pas lesquelles sont fausses

@leo04 ,

Pour être dans $]−π,π[]-\pi,\pi[$ ,
sauf erreur,
dans le 1er cas, k prend les valeurs 0 , 1, -1 -2
dans le 2ème cas, k prend les valeurs 0 , -1

Vérifie en faisant les calculs

je viens de refaire, effectivement.
Merci enormement

De rien @leo04

Ce n'est pas simple lorsqu'on a des absences pour raison de santé.
Alors, bon courage pour rattraper ton retard et reposte si tu as besoin.