Exercice mathématiques fonction dérivé
-
Ggregory dernière édition par mtschoon
Bonjour, j'ai un dernier exercice sur lequel je doute pour la rentrée,
Soit f la fonction dénie sur R − {0} par :
f(x)=x2−5x+2xf(x)=\dfrac{x^2-5x+2}{x}f(x)=xx2−5x+2- Calculer f', la fonction dérivée de f sur R − {0}, et la je trouve -1, ce n'est pas possible si ?
- En déduire le tableau de variations de la fonction f, comme je ne sais pas si la question 1 est juste je préfère ne pas le faire tout de suite
- Construire la courbe représentative de f dans un repère convenablement choisi.
Pourriez-vous jeter rapidement un coup d'oeil ?
Formule re-écrite en Latex par la modération.
-
mtschoon dernière édition par mtschoon

@leo04 , re-bonjour
Est-ce que f(x)=x2−5x+2xf(x)=\dfrac{x^2-5x+2}{x}f(x)=xx2−5x+2 ?
Si c'est bien ce que tu as voulu écrire, f'(x)=-1 est faux...
Utilise la dérivée d'un quotient (voir cours)U(x)=x2−5x+2U(x)=x^2-5x+2U(x)=x2−5x+2 donc U′(x)=2x−5U'(x)=2x-5U′(x)=2x−5
V(x)=xV(x)=xV(x)=x donc V′(x)=1V'(x)=1V′(x)=1Revois ta réponse.
Tu dois trouver f′(x)=x2−2x2f'(x)=\dfrac{x^2-2}{x^2}f′(x)=x2x2−2
-
Ggregory dernière édition par
oui c'est bien ce que je voulais écrire, merci. Ok, je vais refaire le calcul mais oui j'avais trouvé pareille pour u' et v' mais ce résultat m'étonnait
-
Ggregory dernière édition par
f'(x) = (u'xv - uxv')/ve2 = ((2X-5)xX - (Xe2-5X+2)x1)/xe2 donc = (xe2-2)/xe2 ?
-
mtschoon dernière édition par mtschoon

@leo04
Tes écritures ne sont guère lisibles.
Pour écrire les puissances 2, utilise la touche "petit 2" qui doit être en haut à gauche de ton clavier
Pour "x puissance 2", tu obtiens ainsi : x²Ta dérivée est bonne.
-
Ggregory dernière édition par
okay merci, je ferais ça dorénavant. Okay mais comment appliquer cette dérivée pour la question 2 ?
-
mtschoon dernière édition par

@leo04
Le signe de la dérivée te donne le sens de variation de la fonction. (regarde ton cours)
Sur R-{0}, x2>0x^2\gt 0x2>0
Le signe de la dérivée est donc le signe du numérteur x2−2x^2-2x2−2 que tu étudies.
-
Ggregory dernière édition par
c'est positif donc croissant, est-ce correct ?
-
mtschoon dernière édition par

@leo04 ,
Non...
x2−2x^2-2x2−2 n'est pas toujours positif !
-
Ggregory dernière édition par
]-infini;0[ union ]0;+infini[ ?
-
mtschoon dernière édition par

@leo04 ,
On travaille sur ]−∞,0[∪]0,+∞[]-\infty,0[ \cup ]0,+\infty[]−∞,0[∪]0,+∞[ pour que le dénominateur de f (et de f') soi non nul.
Sur cet domaine de définition, trouve le signe de x2−2x^2-2x2−2
C'est un polynôme du second degré.
Trouve ses racines puis applique le théorème relatif au signe d'un polynôme du second degré, ou pratique par factorisation.Tiens nous au courant.
Je regarderai cette après-midi.
-
Ggregory dernière édition par
ok donc delta = b2 - 4ac = 0-4x1x-2 = 8 donc deux racines
x1= -racine8/2 et x2 = racine8/2, c'est donc positif de ]-infini;-racine8/2[,négatif entre les deux racines et de nouveaux positifs après la racine jusque +infini. Est-ce bon ? et pas de souci, répondez quand vous pouvez.
-
mtschoon dernière édition par mtschoon

@leo04 ,
C'est bon.
Les racines se simplifient
x1=82=222=2x_1=\dfrac{\sqrt{8}}{2}=\dfrac{2\sqrt 2}{2}=\sqrt 2x1=28=222=2
x2−=82=−222=−2x_2-=\dfrac{\sqrt{8}}{2}=-\dfrac{2\sqrt 2}{2}=-\sqrt 2x2−=28=−222=−2Remarque , tu aurais pu éviter les formules usuelles
x2−2=0x^2-2=0x2−2=0<=> x2=2x^2=2x2=2 <=> x=±2x=\pm \sqrt 2x=±2L'étude du signe de x2−2x^2-2x2−2 est bon.
-
mtschoon dernière édition par mtschoon

@leo04 ,
Je te joins le tableau de variation correspondant au signe de f'(x) que tu as trouvé
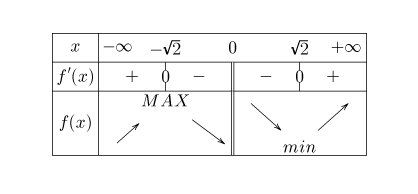
Evidemment, ce n'est pas MAX et min que tu dois écrire.
MAX=f(−2)MAX=f(-\sqrt 2)MAX=f(−2) à calculer
min=f(2)min=f(\sqrt 2)min=f(2) à calculer
-
Ggregory dernière édition par
Merci, le l'avais réalisé et trouvé la même chose, pour la derniere question, je trace un repère sur mon cahier et prend des valeurs de x au hasard ?
-
mtschoon dernière édition par

@leo04 ,
Donne les valeurs de f(−2)f(-\sqrt 2)f(−2) et f(2)f(\sqrt 2)f(2) si tu as besoin d'une vérification.
-
Ggregory dernière édition par
f(-racine2)=-7,8 et f(racine2) =-2,1
-
mtschoon dernière édition par mtschoon

@leo04 ,
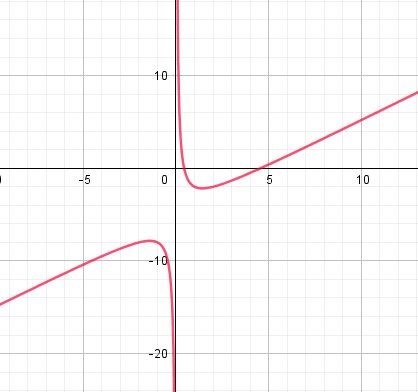
Oui, pour faire le graphique , prends quelque valeurs de x comprises entre --10 et 10 par exemple (-10, ...,,-5, -4, -3 ,...,3 , 4 , 5,..., 10)
Tu dois trouver un graphique ressemblant à ça
-
mtschoon dernière édition par mtschoon

@leo04 ,
Pour f(−2)f(-\sqrt 2)f(−2) et f(2)f(\sqrt 2)f(2) , tes résultats ne sont que des valeurs approchées à 0.1 près.
N'écris pas "=" , mais "voisin de"
f(−2)≈−7.8f(-\sqrt 2)\approx -7.8f(−2)≈−7.8
f(2)≈−2.1f(\sqrt 2)\approx -2.1f(2)≈−2.1
Ces valeurs approchées sont suffisantes pour faire le graphique, mais ce serait mieux de calculer les valeurs exactes que tu mettras dans le tableau de variation (à la place de MAX et min).
-
mtschoon dernière édition par

@leo04 ,
Je te calcule f(−2)f(-\sqrt 2)f(−2)
f(−2)=2+52+2−2=4+52−2=−4+522f(-\sqrt 2)=\dfrac{2+5\sqrt 2+2}{-\sqrt 2}=\dfrac{4+5\sqrt 2}{-\sqrt 2 }=-\dfrac{4+5\sqrt 2}{\sqrt 2}f(−2)=−22+52+2=−24+52=−24+52En principe , on ne laisse pas de radicaux au dénominateur.
On multiplie numérateur et dénominateur par 2\sqrt 22f(−2)=−42+102f(-\sqrt 2)=-\dfrac{4\sqrt 2+10}{2}f(−2)=−242+10
En simplifiant par 2 :
f(−2)=−22−5\boxed{f(-\sqrt 2)=-2\sqrt 2-5}f(−2)=−22−5
Avec le même principe, tu peux calculer f(2f(\sqrt 2f(2)
sauf erreur, tu dois trouver :
f(2)=22−5\boxed{f(\sqrt 2)=2\sqrt 2-5}f(2)=22−5Bons calculs !
-
Ggregory dernière édition par
okay, merci beaucoup en tout cas
-
mtschoon dernière édition par

De rien @leo04
Revois tout ça de près.