Equation de droite triangle

Bonjour
Je n'arrive pas à trouver les équations des droites AB et BC. Pouvez-vous m'aider?

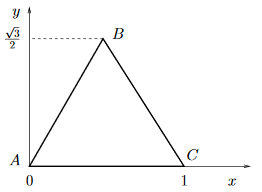
Merci

Bonjour cours,

Quelle est la nature du triangle ABC ?

Si l'énoncé permet de dire que le triangle ABC est équilatéral,
alors pour la droite (AB) : $y = a x$ , à partir des coordonnées du point B, on déduit l'équation de la droite : $y = . . . . .$
Pour la droite (BC), de la forme pour une équation réduite $y = a x + b$ soit on prend les coordonnées des points B et C, soit on indique que la pente est l'opposé de la pente de la droite (AB) et on utilise les coordonnées d'un point.

Noémi merci pour la réponse.
Le triangle est équilatéral.
A partir du point B je remarque que en y = racine(3)/2 et en x=0,5

Y a t'il quelque chose à comprendre aux équations données ? Où c'est juste à apprendre ?

@cours

Tu dois connaitre ces formes d'écritures réduites de droite.
L'équation cartésienne d'une droite s'écrit tous la forme ax+by+c = 0.
Si tu connais un vecteur directeur $u→\overrightarrow{u}$ de la droite et un point (par exemple A) de la droite tu peux utiliser le fait que les vecteurs $AM→\overrightarrow {AM}$ et $u→\overrightarrow{u}$ sont colinéaires.

en fait que je regarde la droite AB je vois que x et y vont fluctuer donc être sûrement dans l'équation mais c'est tout.

@cours

Tu peux vérifier que les coordonnées des points appartenant à la droite sont solutions de son équation.

@Noemi
"il suffit de se placer sur le point correspondant à l’ordonnée à l’origine. Ensuite, on avance d’une unité vers la droite, puis on monte d’autant d’unités que nécessaire pour arriver en un point appartenant à la droite"

J'ai utilisé cette phrase pour calculer AB le problème c'est qu'il n'y pas d'unité sur l’illustration de mon livre de maths, donc j'ai supposé:
y= 0,5x + racine(3)/2

@cours et @Noemi , bonjour

@cours ,

L'équation que tu proposes est inexacte.

Je me permets de lire ce que tu indiques @cours
"il suffit de se placer sur le point correspondant à l’ordonnée à l’origine. Ensuite, on avance d’une unité vers la droite, puis on monte d’autant d’unités que nécessaire pour arriver en un point appartenant à la droite"

Cela sert à trouver le coefficient directeur de la droite de façon "graphique".
Pour appliquer cela, le dessin donné n'est pas suffisant.
Tu dois te placer sur le point A . En avançant à droite d'une unité, tu arrives au point C. C'est à partir du point C d'abscisse 1 qu'il faut remonter pour 'toucher' la droite (AB).
Alors, il faut que tu prolonges (AB) sur ton schéma, et tu trouveras un point d'ordonnée $3\sqrt 3$ .
$3\sqrt 3$ sera le coefficient directeur de la droite (AB)

Remarque :
Il y a un cours clair, sur le site, par calculs, connaissant les coordonnées de deux points, pour trouver l'équation réduite d'une droite sous la forme y=mx+p.
Ici, tu as $A (0, 0)$ , $B(12,32)B(\dfrac{1}{2},\dfrac{\sqrt 3}{2})$ , $C (1, 0)$
En appliquant le cours, tu dois pouvoir trouver les équations de (AB) et (BC)

https://www.mathforu.com/seconde/determiner-equation-droite/

Donne tes réponses si tu as besoin.
Nous vérifierons.

@cours

Pour calculer le coefficient directeur $a$ de la droite (AB), applique la relation :
$\dfrac{y_B-y_A}{x_B-x_A}$

Merci à vous 2.
Pour AB j'obtiens comme droite
(racine(3)/2 ) * 0,5

@cours

Ce n'est pas l'équation d'une droite et pourquoi ce multiplier * ?

en fait j'obtiens par la formule que vous donner :
(racine(3))/2)/(1/2)

@cours ,

C'est ça pour le coefficient direct,, mais ton écriture est compliquée et n'est pas simplifiée.

En appliquant la formule que ton donnes le site , @Noemi et la méthode graphique , le coefficient directeur de la droite (AB) est $m=a=32−012−0=3m=a=\dfrac{\dfrac{\sqrt 3}{2}-0}{\dfrac{1}{2}-0}=\sqrt 3$

(C'est m si tu écrit y=mx+p ou a si tu écrit y=ax+b)

mtschoon c'est bien ce que j'ai obtenu mais c'est la simplification que je n'arrive pas à faire

@cours

Oui $\dfrac{\dfrac{\sqrt3}{2}}{\dfrac{1}{2}} = \dfrac{\sqrt3}{2} \times \dfrac{2}{1} = \sqrt3$

merci c'est que le faisait à l'inverse d'où le *0,5

@cours

Tu as donc l'équation de la droite (AB) : $y=3xy=\sqrt3 x$ .

Détermine maintenant l'équation de la droite (BC).

pour m je trouve -(racine(3))
pour p = (racine(6)/2)=racine(3)

equation = -racine(3)x + racine(3)

@cours

L'équation de la droite (BC) est bien $-\sqrt3 x + \sqrt3$

mais je ne comprends pas d'ou vient le $62\dfrac{\sqrt6}{2}$ ?

P=( $32\frac{\sqrt{3}}{2}$ )-(- $3\sqrt{3}$ *1/2)
= $32\frac{\sqrt{3}}{2}$ -(- $22\frac{\sqrt{2}}{2}$ )
= $32\frac{\sqrt{3}}{2}$ + $32\frac{\sqrt{3}}{2}$ = $62\frac{\sqrt{6}}{2}$ = $3\sqrt{3}$

@cours ,
Il y a une petite faute de frappe à la seconde ligne
Je pense que tu as voulu écrire
$P=32−(−32)P=\dfrac{\sqrt 3}{2}-(-\dfrac{\sqrt 3}{2})$

(Bravo pour le latex !)

C'est exact. Merci

@cours

Attention :
$32+32\dfrac{\sqrt{3}}{2}+\dfrac{\sqrt{3}}{2}$ n'est pas égal à $62\dfrac{\sqrt{6}}{2}$
mais à $2×322\times \dfrac{\sqrt{3}}{2}$ soit à $3\sqrt{3}$

@cours ,

Une autre remarque pour (BC)

Pour l'équation de (BC) , lorsque tu as trouvé $y=−3x+py=-\sqrt 3x+p$

Tu as utilisé le point B , d'où calcul pas très simple; voir la remarque de Noemi qui t'a signalé une confusion entre $6\sqrt 6$ qui vaut $23\sqrt 2\sqrt 3$ et $232\sqrt 3$

Au passage, si tu veux revoir les propriétés des racines carrées, regarde ici :
https://www.mathforu.com/troisieme/reduction-et-racines-carrees/

Si tu avais utilisé le point C (1,0), tu aurais obtenu directement
$0=−3×1+p0=-\sqrt 3 \times 1+p$ <=> $p=3p=\sqrt 3$

Bon travail !