exercice étude énergétique

Bonjour,

Pouvez-vous m'aider à faire cet exercice qui me pose problème ?

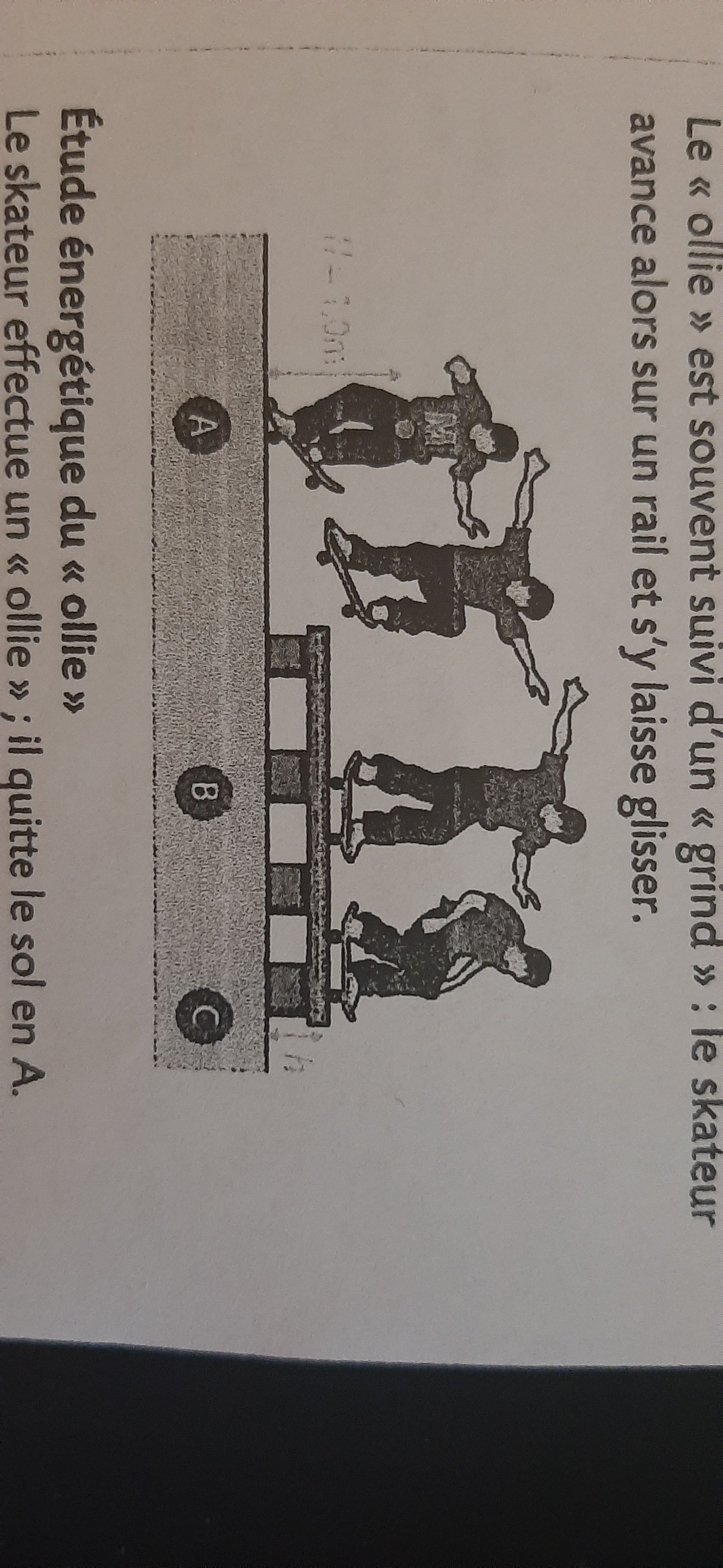
Au skateboard, un « ollie » est un saut effectué avec la planche.
Pour réaliser cette figure, il faut donner un coup avec le pied arrière de manière à faire « claquer » l'arrière de la planche.
Le décollage est alors possible. Le « ollie » est souvent suivi d'un « grind » : le skateur avance alors sur un rail et s'y laisse glisser.

Étude énergétique du « ollie » Le skateur effectue un « ollie »; il quitte le sol en A. Sa vitesse a pour valeur vA=4,20 m.s ; il atteint le rail en B avec la vitesse vg.

On néglige les frottements et l'action de l'air sur le parcours AB.

Donner les expressions de l'énergie mécanique du skateur en A puis en B.

A : Em = Ec(a) + Ep(a) ?? Si c'est ça j'ai juste à remplacer par des valeurs numériques ?

B: Em = Ec(b) + Ep(b) ??

Cette énergie mécanique varie-t-elle entre A et B?

Oui car au début le skateur est sol et est ensuite plus haut et sur une barre en métal

3.a. Exprimer la valeur de la vitesse vB en fonction de g, h et vA.

Montrer que vB = 2,8 m s

Faut-il prendre pour cette question la formule de calcul d'une chute libre ?
v = √[2×g×h] même si ça m'étonnerait fortement

Étude énergétique du « grind » Sur le rail, le système est soumis à une force de frottement de valeur constante f=30,0 N.

Déterminer la distance BC parcourue par le skateur jusqu'à son arrêt complet sur la barre.

C'est surtout cette question qui me pose problème, j'imagine qu'il y a un rapport entre la masse les frottements et l'inclinaison de la barre qui est ici parfaitement droite ?

Données : hauteur du rail h = 50 cm g = 9.81 N/Kg
Masse du système m = 80.0 kg

Merci.

Bonjour Nico18,

Remplace l'énergie cinétique et l'énergie potentielle par leur expression en fonction de la masse, la vitesse et la hauteur.
Comme on néglige les frottements, l'énergie mécanique se conserve, donc ne varie pas.
Utilise le fait que $Em_A = Em_B$ . Tu dois retrouver la formule du calcul pour une chute libre.

Etude énergétique du "grind"
Tu appliques le même raisonnement que pour l'exercice précédent.

@Nico18 a dit dans exercice étude énergétique :

v = √[2×g×h]

1 Em(A) = EC = 0,5 x mv2 + Ep = m x g x (z1 - z0) du coup c'est juste les expressions j'ai besoin de remplacer par les valeurs numériques de l'énoncé ou pas ?

Ah oui d'accord
La formule pour la chute libre = v = √[2×g×h]

@Nico18

Tu dois écrire l'énergie mécanique en A puis en B.
Il est juste demandé les expressions, donc tu peux remplacer dans le cas ou c'est nul.

Question 3, tu utilises la relation $Em_A=Em_B$ pour déterminer la relation entre les vitesses.
Tu trouves une formule voisine de celle de la chute libre. Cette formule comprend la vitesse $v_B$ .

Mais les expressions sont les mêmes non ? comment ça dans le cas ou c'est nul ?

Ah d'accord la relation EmA = EmB me donne une formule similaire à celle de la chute, donc il faut que je trouve le même nombre en J pour l'énergie mécanique A et B ? Si oui je sais pas trop comment faire fin comment chercher la formule surtout si on utilise vB

@Nico18

Au point A, pas d'énergie potentielle donc $EmA=12mvA2Em_A=\dfrac{1}{2} mv_A^2$
Au point B, $EmB=12mvB2+mghEm_B=\dfrac{1}{2} mv_B^2+ mgh$

Tu as donc $12mvA2=12mvB2+mgh\dfrac{1}{2} mv_A^2=\dfrac{1}{2} mv_B^2+ mgh$
en simplifiant
$v_A^2 = v_B^2 + 2gh$
tu en déduis $v_B$

Tu exprimes ensuite la variation d'énergie mécanique entre le point B et le point C qui est égale au travail de la force de frottement.

Bonjour Noemi,

Encore merci pour votre aide précieuse

Si j'ai bien compris à la question 3) b) il faut juste que je fasse une petite équation ? avec vA² = vB² + 2gh et donc inverser vA² et vB² ?

@Nico18

Tu isoles $v_B$ de l'équation soit $v_B^2 = v_A^2 - 2gh$ .
Tu effectues ensuite le calcul.

vB² = 4.20² - 2 x 9.81 x 0.05
= 16.659
= racine carré de 16.659
= 4.08 ?

Je trouve pas vB = 2.8 m/s

@Nico18

Une erreur pour h : h = 50 cm = 0,5 m.

Pour la 4 par contre il y a les frottements pris en compte f = 30.0 N

et f = m x a ? la masse x l'accélération mais le du fait qu'il ralenti c'est pas plutôt la décélération ??

@Nico18

Pour la question 4, tu appliques : la variation de l'énergie mécanique = travail des forces de frottements.

D'accord sachant que dans ce cas là, la force des frottements est constante elle est donc conservative puisqu'elle ne dépend pas du chemin suivit donc (delta)Em = 0, donc si mon raisonnement est correct (delta)Ec + (delta)Epp = 0
(delta)Ec = (1/2)m x vc² - (1/2)m x vb² + m x g x zc - m x g x zb = 0 , ça vous semble juste ?

@Nico18

Non,

$ΔEm=f×d\Delta E_m= f\times d$

ah bon d'accord j'ai essayé de trouver un raisonnement logique
f on l'a c'est 30.0 mais la distance reste à déterminer d = (delta)Em x -f ?

@Nico18

Non : $\dfrac{\Delta E_m}{f}$

On calcule (delta)EM = Ec + Epp ?

@Nico18

$ΔEm=EC1+Ep1−EC2−Ep2\Delta E_m=E_{C1} + E_{p1} - E_{C2} - E_{p2}$

D'accord mais ec2 + ep2 est égal à 0 non ? Car la vitesse au point c'est sera de 0

@Nico18
Oui $E_{C2} = 0$

Vu que la barre est horizontale, l'équation devient :
$12mvB2=f×d\dfrac{1}{2} mv_B^2 = f\times d$ ,
Tu isoles $d$ et tu fais le calcul.

D = (1/2)x80x2.8(au carré) / 30

= environ 10.5 metre ça me parait beaucoup non ?

@Nico18 a dit dans exercice étude énergétique :

D = (1/2)x80x2.8(au carré) / 30

= environ 10.5 metre ça me parait beaucoup non ?

Hors exercice, juste pour répondre à ta question : "environ 10.5 metre ça me parait beaucoup non ?"

Le ralentissement du skater est en réalité du à 2 forces, la force de frottement aérodynamique du skater dans l'air et la force de résistance au roulement (le skate roule, il ne glisse pas).

Evaluation d le force de frottement aérodynamique du skater dans l'air (à 2,8 m/s) : Fa = 1/2 * Rho(air) * Cx * S * v²
Fa = 1/2 * 1,3 * 0,8 * 1 * 2,8² = 4 N
Cette force diminue avec la vitesse ... en pratique, elle est négligable devant la force de frottement annoncée de 30 N
... donc, la force qui ralentit le skateur est quasi uniquement la force de résistance au roulement, cette force est proportionnelle au poids.

On a donc 30 = k809,81
k = 0,038 (soit 3,8 %)
Juste pour info, la valeur de k pour une "voiture" normale sur route normale est de l'ordre de 1,5 %
Et k diminue si le "pneu" est plus dur ... donc, pour un bon skate (les roues sont bien plus "dures" qu'un pneu de voiture), on devrait avoir k très sensiblement < 1,5 %
Et donc, sur un bon skate ... la distance parcourue sur une surface horizontale devrait être très sensiblement supérieure aux 10,5 m que l'on trouve à partir des données de l'énoncé.

@Nico18

Le calcul est correct.

Nickel merci beaucoup Noemi et Black-Jack pour votre aide