Dis si les vecteurs AB et DC sont colinéaires
-
Aali dernière édition par
Svp aidez moi pour mon exercice
ÉNONCÉ : dans chacune des cas suivants dis si les vecteurs AB et DC sont colinéaires :
A(1;-3) ; B(-4;8) ; C(-6;2) et D(0;2)A(5;5) ; B(0;-1) ; C(10;11) et D(5;6)
A(9;1) ; B(6;-1) ; C(3;-3) et D(1;2)
-
Bonjour ali, (Marque de politesse à ne pas oublier !!)
Détermine les coordonnées des vecteurs et vérifie la relation du cours qui te permet de justifier si deux vecteurs sont colinéaires.
Indique tes éléments de réponse si tu souhaites une correction.
-
Aali dernière édition par
@Noemi
Ok merci beaucoup
-
Peux-tu indiquer la propriété du cours pour des vecteurs colinéaires ?
-
Aali dernière édition par

-
Tu appliques donc cette propriété
Le corrigé pour le premier calcul :
AB→=(−4−1;8−(−3))=(−5:11)\overrightarrow{AB}=(-4-1 ; 8-(-3))=(-5:11)AB=(−4−1;8−(−3))=(−5:11)
DC→=(−6−0;2−2)=(−6;0)\overrightarrow{DC}=(-6-0;2-2)=(-6;0)DC=(−6−0;2−2)=(−6;0)
le calcul de xy′−x′yxy'-x'yxy′−x′y donne :
xy′−x′y=(−5)×0−(−6)×11)=0+66=66xy'-x'y=(-5)\times0-(-6)\times11)=0+66=66xy′−x′y=(−5)×0−(−6)×11)=0+66=66
On déduit xy′−x′yxy'-x'yxy′−x′y différent de 0, donc les deux vecteurs ne sont pas colinéaires.Applique le même raisonnement pour les deux autres cas.
Tu peux écrire tes résultats si tu souhaites une correction.
-
Aali dernière édition par
@Noemi
Ok merci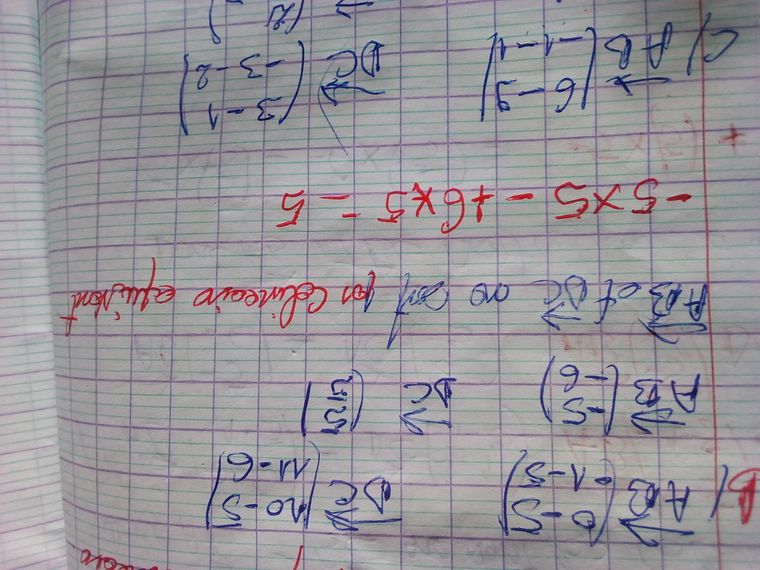
-
Le document est incomplet mais la démarche est correcte.
Tu dois trouver pour chaque cas que les vecteurs ne sont pas colinéaires.