Dis si les droits (AB) et (CD) sont perpendiculaires et justifier votre réponse

[ali]

Bonjour svp aide moi à traiter mais exercice
ÉNONCÉ : dans chacune des cas suivants dis si les droits (AB) et (CD) sont perpendiculaires et justifier votre réponse

A(3;-1) ; B(-2;1) ; C(0;5) D(2;10)

A(√3;3) ; B(-1;2√3) ; C(0;0) ; D(2;1)

[Noemi]

Bonjour ali,

Démontre que les vecteurs $\overrightarrow{AB}$ et $\overrightarrow{CD}$ sont orthogonaux , soit que $x{x}^{\prime }+y{y}^{\prime }=0$.
Premier cas :
$\overrightarrow{AB}$=(-5;2)$ et
$\overrightarrow{CD}$=(2;5)
$x{x}^{\prime }+y{y}^{\prime }=(-5)\times 2+2\times 5=0$
Conclusion : les deux vecteurs sont orthogonaux.

Applique le même raisonnement pour le deuxième.

Indique tes calculs si tu souhaites une correction.

[ali]

@Noemi
Ok merci beaucoup mais pour le √3 c'est difficile pour moi

[mtschoon]

@ali et @Noemi , bonjour,

@ali, je te donne quelques indications pour ta seconde question.
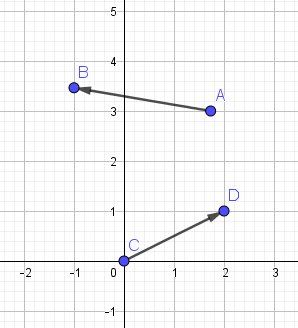
Si tu places, avec leurs coordonnées, les points dans un repère, tu peux déjà constater que les vecteurs ne sont pas orthogonaux
.

Pour le prouver, tu utilises la méthode indiquée par @Noemi

$A(\sqrt{3},3)$
$B(-1,2\sqrt{3})$
Donc $\overrightarrow{AB}(-1-\sqrt{3},2\sqrt{3}-3)$

$C(0,0)$
$D(2,1)$
Donc $\overrightarrow{CD}(2,1)$

Tu calcules $x{x}^{\prime }+y{y}^{\prime }$.

Après développement et simplification, tu dois, sauf erreur, trouver $-5$

$-5\ne 0$, d'où la conclusion

Reposte si besoin.

[Noemi]

@ali

$A(\sqrt{3},3)$
$B(-1,2\sqrt{3})$
$\overrightarrow{AB}(-1-\sqrt{3},2\sqrt{3}-3)$
$C(0,0)$
$D(2,1)$
$\overrightarrow{CD}(2,1)$

Tu calcules $x{x}^{\prime }+y{y}^{\prime }=(-1-\sqrt{3})\times 2+(2\sqrt{3}-3)\times 1$
$=-2-2\sqrt{3}+2\sqrt{3}-3=-5$.
Tu conclus $x{x}^{\prime }+y{y}^{\prime }\ne 0$ donc les vecteurs .......... ..