La fonction inconnue (j'ai mis en gras et italique ce que je pense avoir compléter)
-
Thé.brt dernière édition par
On considère la fonction f dont la courbe représentative est tracée ci-dessous.
On a également tracé sa tangente au point d'abscisse 2
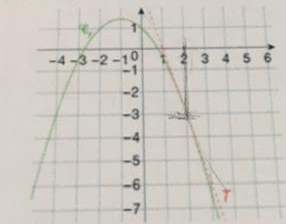
1) A l'aide du graphique, donner le tableau de variation de f
2) Par lecture graphique, donner les valeurs de f(0), f(2) et f'(2)
3) On admet que f(x)=ax2+bx+c
a) calculer f'(x)
b)montrer que a, b et c vérifient le système suivant
c)En résolvant ce système, montrer que :
f(x)=-0,5x2-x+1
4)Retrouver par le calcul le tableau de variation de f.
-
Bonjour Thé-brt,
f′(2)f'(2)f′(2) correspond au coefficient directeur de la tangente au point d'abscisse 2.
Pour la question 2, le calcul de la dérivée, tu dois appliquer :
Si f(x)=x2f(x) = x^2f(x)=x2, f′(x)=2xf'(x) = 2xf′(x)=2x
si f(x)=ax+bf(x) = ax+bf(x)=ax+b, f′(x)=af'(x) = af′(x)=a
-
Thé.brt dernière édition par
@Noemi Alors je ne l'ai pas mis en gras car j'avais de gros doutes, mais j'avais déterminer que c'était -3
-
C'est bien -3.
Calcule la dérivée.
-
Thé.brt dernière édition par
@Noemi Alors justement qu'es ce que la dérivée ?
-
Thé.brt dernière édition par
Ha je crois avoir compris cette partie
-
Tu n'as pas une définition dans ton cours ?
En voici une : On appelle dérivée de la fonction fff au point d'abscisse x0x_0x0 la limite, si elle existe, du rapport de l'accroissement Δy\Delta yΔy de la fonction à l'accroissement Δx\Delta xΔx de la variable lorsque ce dernier tend vers zéro.Pour le calcul, tu utilises les indications de mon premier post.
Tu dois trouver f′(x)=2ax+bf'(x) = 2ax + bf′(x)=2ax+b.
Indique si tu ne comprends pas
-
Thé.brt dernière édition par
Cela donne 2a+b?
-
Non
La dérivée de ax2ax^2ax2 est 2ax2ax2ax et la dérivée de bx+cbx+cbx+c est bbb.
donc
f′(x)=2ax+bf'(x) = 2ax + bf′(x)=2ax+bPour la question b), tu utilises les résultat de la question 2).
Pour f(0)=1f(0) = 1f(0)=1 comme f(x)=ax2+bx+cf(x) = ax^2+bx+cf(x)=ax2+bx+c
si tu remplaces xxx par 0 le résultat donne 1.
soit a×02+b×0+c=1a\times 0^2 + b\times 0 + c = 1a×02+b×0+c=1
en simplifiant cela donne c=1c = 1c=1.Indique tes calculs si tu souhaites une correction ou une question si tu ne comprends pas.
-
Thé.brt dernière édition par
Ha... merci