Cercle trigonométrique et produit scalaire

[mousaka]

bonjour mon énonce est: sur un cercle trigonométrique de centre O on place les points A et B associé a pi/4 et pi/3
en calculant de DEUX manières le produit scalaire de OAxOB determiner la valeur de cos pi/12
je pensais pour calculer le produit scalaire d'utiliser la formule dans un repère mais l'autre manière je sais pas et j'aimerai savoir comment calculer cette valeur de cos pi/12
merci dans l’attente de votre réponse

[Noemi]

Bonjour mousaka,

Ecris les formules pour le produit scalaire.
$\overrightarrow{OA}.\overrightarrow{OB}=.....$

[mousaka]

mais je sais pas quelle formule utiliser justement

[Noemi]

$\overrightarrow{OA}.\overrightarrow{OB}=OA\times OB\times cos(\overrightarrow{OA},\overrightarrow{OB})$

[mousaka]

peut etre que OAOB=xx'yy'

[Noemi]

La deuxième est bien :
$\overrightarrow{OA}.\overrightarrow{OB}=x{x}^{\prime }+y{y}^{\prime }$

[mousaka]

du coup la formule dans le plan serait la seconde manière ?

Et es ce que pi/4 et pi/3 serait la longueur OA et OB ?

[Noemi]

Non,

Les points A et B sont sur le cercle trigonométrique donc OA = OB = 1

L'angle $(\overrightarrow{OA},\overrightarrow{OB})=\frac{\pi }{3}-\frac{\pi }{4}=...$

[mtschoon]

Bonjour @Noemi et @mousaka

@mousaka , je t'explicite un peu plus l'idée de l'énoncé vu que tu n'as pas l'air d'avancer.

Schéma :

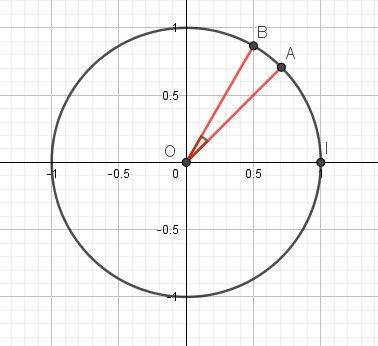
Si tu lis les indications données par @Noemi , tu as tout ce qu'il faut pour aboutir.

Avec la première façon :
$\overrightarrow{OA}.\overrightarrow{OB}=OA\times OB\times cos(\frac{\pi }{12})$
( Comprends pourquoi $\frac{\pi }{12})$

Donc
$\overrightarrow{OA}.\overrightarrow{OB}=1\times 1\times cos(\frac{\pi }{12})=\boxed{cos(\frac{\pi }{12})}$

Avec la seconde façon:
$\overrightarrow{OA}.\overrightarrow{OB}=\boxed{X{X}^{\prime }+Y{Y}^{\prime }}$

D'où $\boxed{cos(\frac{\pi }{12})=X{X}^{\prime }+Y{Y}^{\prime }}$

Il te reste donc à calculer $X{X}^{\prime }+Y{Y}^{\prime }$

$X=x_A-x_O=cos(\frac{\pi }{4})-0=cos(\frac{\pi }{4})=\frac{\sqrt{2}}{2}$

$X^{\prime }=x_B-x_O=cos(\frac{\pi }{3})-0=cos(\frac{\pi }{3})=\frac{1}{2}$

$Y=..................$ (à faire)

$Y^{\prime }=.................$ (à faire)

Tu pourras ainsi tirer la conclusion sur la valeur exacte de $cos(\frac{\pi }{12})$

Tiens nous au courant si tu as besoin.