Dérivés : Consommation d’essence
-
Alexis Dumont dernière édition par

Bonjour à tous, j’aimerais obtenir de l’aide sur cet exercice :
La consommation d’essence C d’un véhicule peut s’exprimer en fonction de la vitesse v sous la forme :
C(v)= 0,06v + 150/v, avec v > 0.
-
Calculer l’expression de C’ , fonction dérivée de la fonction C ]0 ; ∞[
-
Déterminer le signe de C’(v) pour v > 0
-
Donner le tableau de variations de la fonction C sur l’intervalle [20 ; 130].
-
En déduire la vitesse à laquelle il faut rouler pour que la consommation soit minimale. Quelle est cette consommation.
Je vous remercie par avance, je n’ai pas de résultat pour le moment car je ne sais pas du tout comment commencer.
-
-
Bonjour Alexis-Dumont,
La dérivée de ax+bax+bax+b est aaa donc la dérivée de $0,06v est .....
La dérivée de ax\dfrac{a}{x}xa est −ax2-\dfrac{a}{x^2}−x2a donc la dérivée de 150v\dfrac{150}{v}v150 est ....Tu déduis C′(v)=....C'(v) = ....C′(v)=....
Complète les .....
-
Alexis Dumont dernière édition par

Du coup, la dérivée de 0,06v est 0,06 et la dérivée de 150/x est -150/v^2 ?
Donc C’(v) = 0,06 - 150/v^ 2 ?
-
La dérivée est juste.
Détermines son signe en réduisant l'expression au même dénominateur.
-
Kenza Mansouri dernière édition par

Ce message a été supprimé !
-
Alexis Dumont dernière édition par

@Noemi Je ne sais pas comment on fait...

-
mtschoon dernière édition par mtschoon

Bonjour,
Un coup de pouce pour avancer ton travail,
Je suppose que C(v)=0.06v+150vC(v)=0.06v+\dfrac{150}{v}C(v)=0.06v+v150
C′(v)=0.06−150v2C'(v)=0.06-\dfrac{150}{v^2}C′(v)=0.06−v2150
En réduisant au même dénominateur :
C′(v)=0.06v2−150v2C'(v)=\dfrac{0.06v^2-150}{v^2}C′(v)=v20.06v2−150
Tu dois étudier le signe de C′(v)C'(v)C′(v) pour v>0v\gt 0v>0
Le dénominateur v2v^2v2 est strictement positif, donc C′(v)C'(v)C′(v) est du signe du numérateur 0.06v2−1500.06v^2-1500.06v2−150
C′(v)=0C'(v)=0C′(v)=0 <=> 0.06v2−150=00.06v^2-150=00.06v2−150=0 <=> v2=2500v^2=2500v2=2500
Au final,
C′(v)=0C'(v)=0C′(v)=0 <=> v=2500v=\sqrt{2500}v=2500 <=> v=50v=50v=50
Il te reste à faire :
C′(v)>0C'(v) \gt 0C′(v)>0 <=> ..................(tu calcules)
C′(v)<0C'(v) \lt 0C′(v)<0 <=> ..................(tu calcules)
-
Alexis Dumont dernière édition par

@mtschoon
Bonjour, merci beaucoup ! Mais j’ai pas compris pourquoi de 0,06v^2 c’est passé à 0,05v^2 ? Merci
-
C'est une erreur de frappe. C'est bien 0,06v2−150=00,06v^2 - 150 = 00,06v2−150=0 qu'il faut lire.
-
Alexis Dumont dernière édition par Alexis Dumont

Ok merci ! V vaut bien 50 ?
-
mtschoon dernière édition par mtschoon

Exact, faute de frappe pour 0.005 au lieu de 0.006.
(j'ai rectifié)
0.06v2−150=00.06v^2-150=00.06v2−150=0 <=> v2=1500.06v^2=\dfrac{150}{0.06}v2=0.06150 <=> v2=2500v^2=2500v2=2500 d'où, vu que v est positif :
v=50v=50v=50
-
Alexis Dumont dernière édition par

Aucun problème merci beaucoup ! Par contre je n’ai pas bien compris comment calculer c’(v)>0 et c’(v) < 0
-
mtschoon dernière édition par mtschoon

v étant positif dans ton énoncé , cela ne doit pas te poser de difficultés.
C′(v)>0C'(v)\gt 0C′(v)>0 <=> 0.06v2−150>00.06v^2-150 \gt 00.06v2−150>0 <=> v2>1500.06v^2\gt \dfrac{150}{0.06}v2>0.06150 , c'est à dire :
v2>2500v^2\gt 2500v2>2500
En prenant la racine carrée de chaque membre positif ( on ne change pas le sens de l'inégalité) , on obtient v>50v\gt 50v>50
Tu traites de la même façon le cas C′(v)<0C'(v)\lt 0C′(v)<0
-
Alexis Dumont dernière édition par

Alors,
C’(v) < 0 <=> 0,06 v^2 - 150
<=> v^2 < 150/0,06
V^2 < 2500
V< 50 ?
-
mtschoon dernière édition par

Il faut écrire 0.06v2−150<00.06v^2-150 \lt 00.06v2−150<0
v2<2500v^2\lt 2500v2<2500
Ensuite, il faut préciser que tu travailles pour x>0x \gt 0x>0, donc qu'en prenant la racine carrée de chaque membre , tu trouves :
0<v<500\lt v \lt 500<v<50
-
Alexis Dumont dernière édition par

Ok merci, est-ce que je dois donner son tableau de signe ?
-
mtschoon dernière édition par

Faire un tableau des signes de C'(v) sera très bien pour la conclusion de la question 2 (et tu pourras t'en servir pour le tableau de variations demandé à la question 3)
-
Alexis Dumont dernière édition par

Merci beaucoup, pour la question 3 j’ai fait ce tableau.
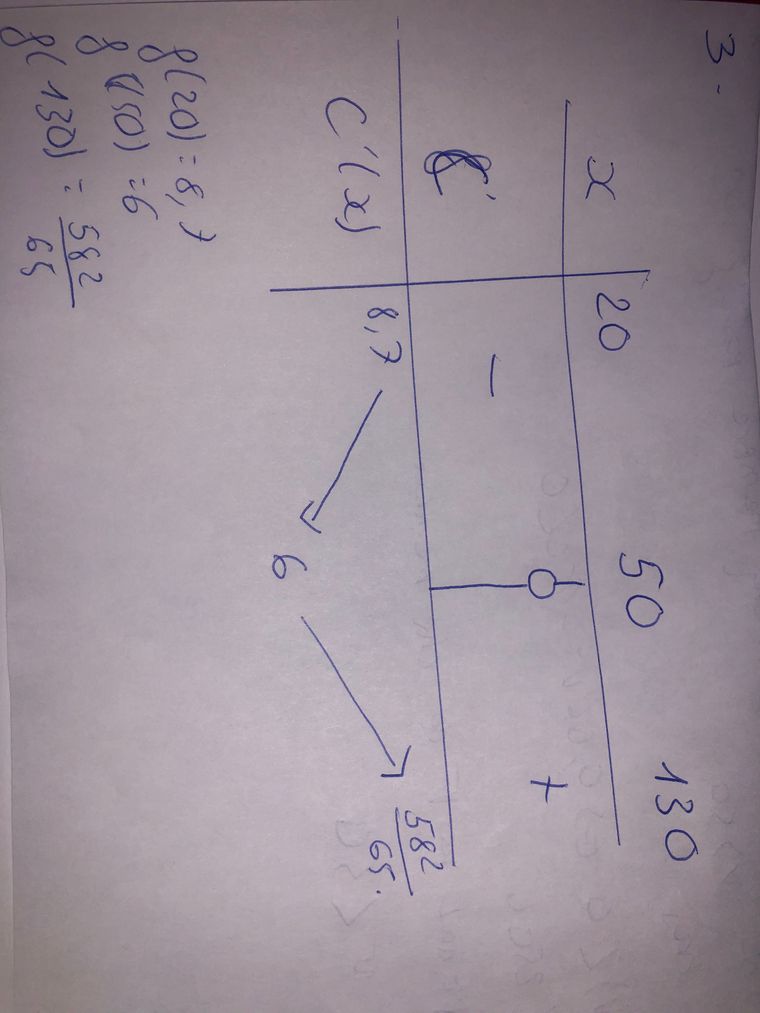
Et pour la question 4:
La consommation admet un minimum en 50, alors pour que la consommation soit minimale, il faudrait rouler à 50km/h. Cette consommation est 6
-
mtschoon dernière édition par

C'est bon !
-
Alexis Dumont dernière édition par Alexis Dumont

Merci beaucoup pour votre aide !! Est-ce que la consommation a une unité ?
-
Alexis Dumont dernière édition par

Et aussi juste pour être sûr, pour la question 2, j’écris :
C(v)= 0,06 v + 150/v
C’(v)= 0,06 - 150/v^2En réduisant au même dénominateur :
C’(v)= 0,06 v^2 - 150 / v^21er cas:
C’(v) > 0 <=> 0,06 v^2 - 150 > 0 <=>
V^2 > 150 / 0,06 c’est à dire,
V^2 > 2500
En prenant la racine de chaque membre positif, on obtient v > 502e cas:
C’(v) < 0 <=> 0,06v^2 - 150 < 0
V^2 < 2500
En prenant la racine de chaque membre,
0<v>50 ?
-
mtschoon dernière édition par

-
Alexis Dumont dernière édition par

Mince erreur d’inattention !! Merci
-
mtschoon dernière édition par

@Alexis-Dumont , de rien !
C'est très bien si tu maîtrises l'étude de la fonction.Bon travail !