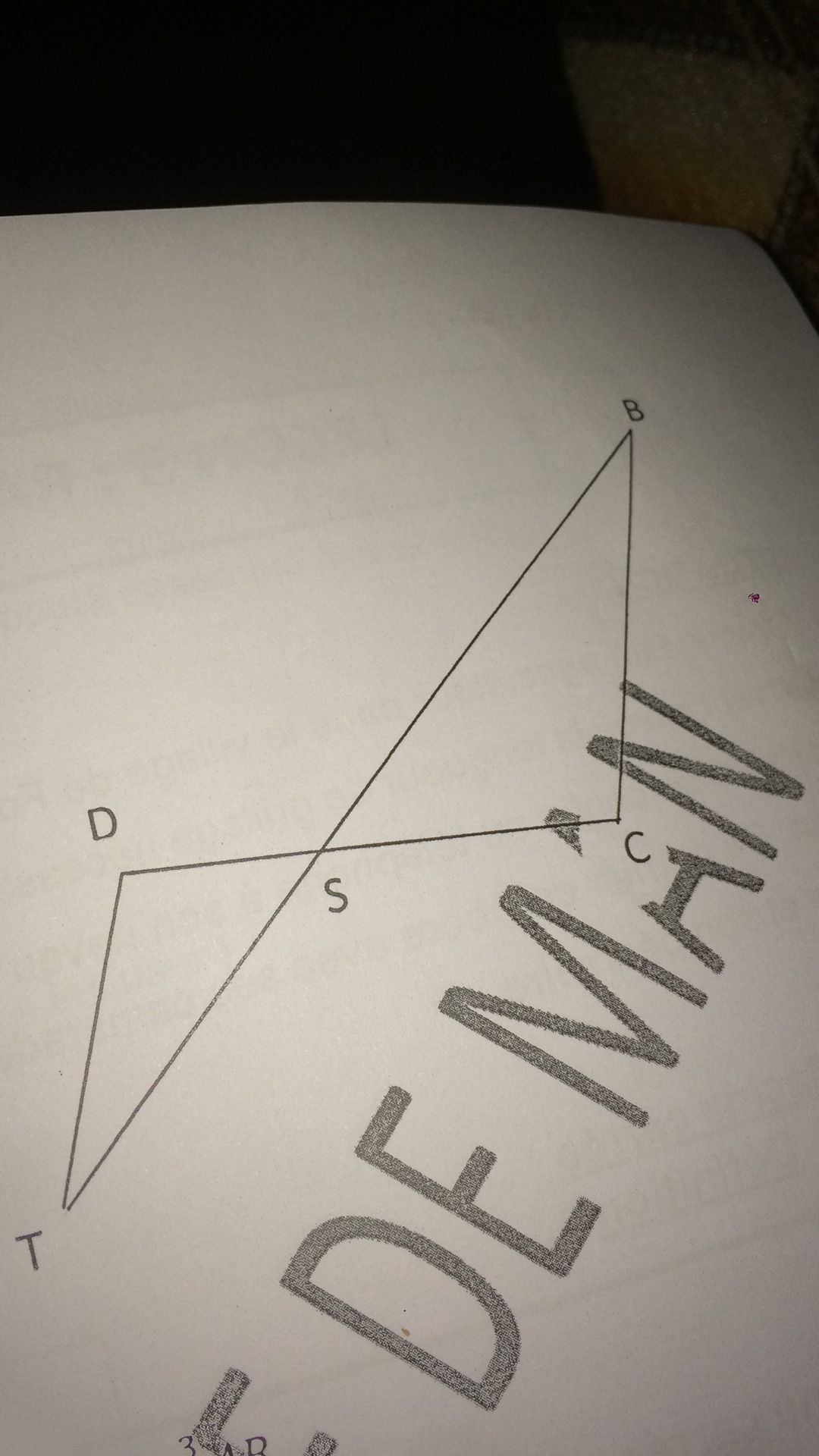
Thalès : configuration avec des triangles

[ali]

Bonsoir à tous un petit exercice qui me fatigue
S est un point de segement [DC] tel que:DS$\frac{1}{3}$DC

Les droit (DT) et (BC) sont parallèles. On donne: DT=3

1. démontre que:SC=$\frac{2}{3}$DC

2. démontre que:BC=6

[Noemi]

Bonsoir ali,

As-tu fait une figure ?
$DS=\frac{1}{3}DC$, tu en déduis $SC$.

Pour le calcul de $BC$ utilise la propriété de Thalès.
$\frac{BC}{DT}=\frac{SC}{DS}$

[ali]

@Noemi effectivement il y’a un figure mais je ne sait pas comment le mettre sur le lien

[ali]

@Noemi stp comment en déduis SC maintenant

[ali]

@Noemi

[ali]

@Noemi stp le sujet nous parle de démontre

[Noemi]

@ali
$DS=\frac{1}{3}DC$, et comme les points D, S et C sont alignés dans cet ordre : $DS+SC=DC$
$\frac{1}{3}DC+SC=DC$ donc $SC=....$

Pour le calcul de $BC$ utilise la propriété de Thalès pour les triangles BSC et TSD.

$\frac{BC}{DT}=\frac{SC}{DS}$

Soit $\frac{BC}{3}=\frac{SC}{DS}$ et $\frac{SC}{DS}=\frac{2}{3}\times \frac{3}{1}=2$
Tu déduis $BC$.