Justifier que les droites (MN) et (BC) sont parallèles
-
Aali dernière édition par Noemi
Bonjour à tous le monde svp je n’arrive pas a traiter ce t’erci
- les droites (BM) et (BC) se coupent en A
- AMAB\frac{AM}{AB}ABAM=0,83 et ANAC\frac{AN}{AC}ACAN=0,83
Justifier que les droites (MN) et (BC) sont parallèles 
-
mtschoon dernière édition par mtschoon

@ali , bonjour,
Ton insertion d'image n'a pas fonctionné
Tu as dû faire aussi des erreurs en écrivant l'énoncé.Tu écris "les droites (BM) et (BC) se coupent en A" : cela n'a pas de sens car, B étant commun à (BM) et (BC), forcément si (BM) et (BC) ne sont pas confondues, c'est en B qu'elles se coupent.
Merci de rectifier tout ça.
-
mtschoon dernière édition par mtschoon

@ali , ta question semble être l'application directe du Théorème de Thalès (plus précisément la réciproque du tiéorème de Thalès appliquée au triangle )
AMAB=ANAC\dfrac{AM}{AB}=\dfrac{AN}{AC}ABAM=ACAN implique (MN)//(BC)(MN)//(BC)(MN)//(BC)
Je te mets un lien :
https://www.mathforu.com/troisieme/le-theoreme-de-thales/
(regarde le paragraphe II)Tu devrais avoir un schéma ressemblant un peu à celui là:
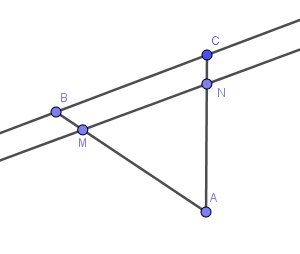
-
Aali dernière édition par
@mtschoon merci d’avoir essayé main le triangle que tu a tracé n’E pas sa
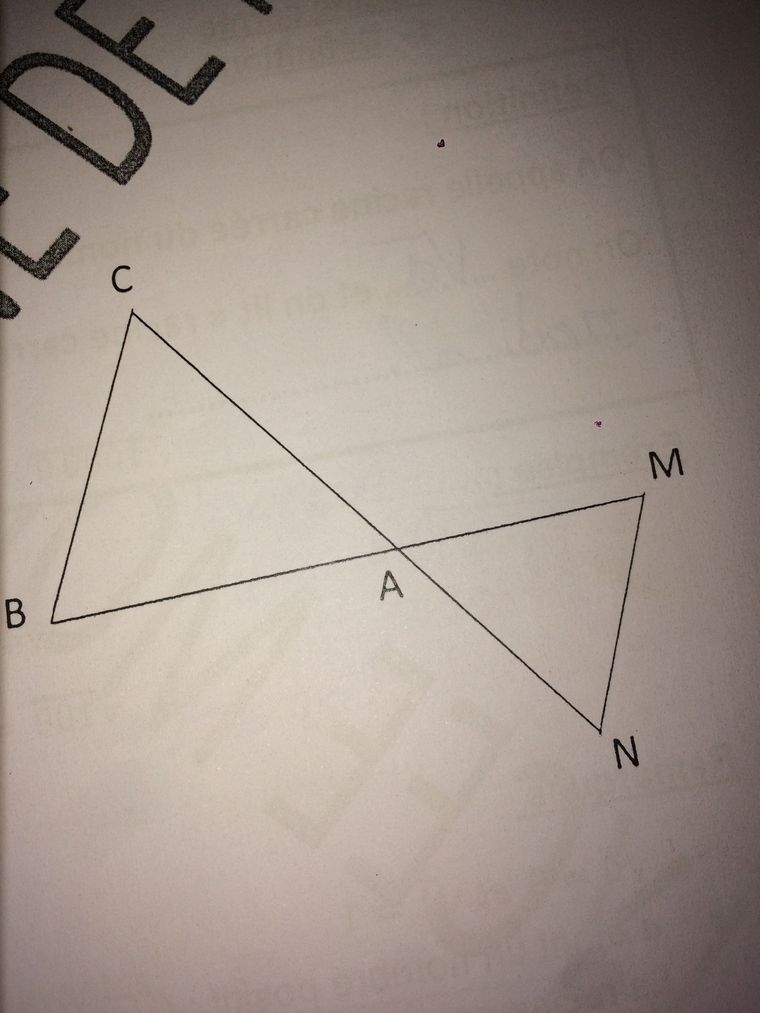
-
Bonjour ali,
Utilise comme indiqué par mtschoon, la réciproque de la propriété de Thalès.
-
Aali dernière édition par
@mtschoon ok stp la justification
-
La réponse a été donnée :
AMAB=ANAC=0,83\dfrac{AM}{AB}=\dfrac{AN}{AC}= 0,83ABAM=ACAN=0,83 et les points BBB, AAA MMM, et CCC, AAA, NNN sont alignés dans le même ordre sur deux droites sécantes en AAA, alors les droites (MN)(MN)(MN) et (BC)(BC)(BC) sont parallèles.
-
mtschoon dernière édition par mtschoon

@ali , bonsoir,
Merci pour ton schéma.
Je t'avais dit de consulter le paragraphe II du lien que je t'ai donné (partie COURS du site)
Visiblement, tu n'y es pas allé voir.Regarde ce qui est indiqué sur le site (j'ai fait une copie d'écran) :

Et au dessous, il y a les schémas associés, alors , va voir.Comme te l'a déja dit Noemi, dans ton exercice, respectivement sur les droites (AM) et (AN ), les points B,A,MB,A,MB,A,M et C,A,NC,A, NC,A,N sont alignés dans le même ordre .
L'égalité des rapports :AMAB=ANAC=0.83\dfrac{AM}{AB}=\dfrac{AN}{AC}=0.83ABAM=ACAN=0.83 , te permet de conclure que : (MN)//(BC)(MN)//(BC)(MN)//(BC)C'est tout pour la justification .
La justification consiste seulement à appliquer directement cette propriété qui est la réciproque du théorème de Thalès appliqué aux triangles.
-
Aali dernière édition par
@mtschoon merci Énormément






-
Aali dernière édition par
@Noemi merci

 beaucoup de m’avoir aidé
beaucoup de m’avoir aidé
-
mtschoon dernière édition par

@ali , de rien et bon travail !