Calibrage statique - étalonnage
-
Ddut dernière édition par
Bonjour,
Je bloque sur un calcul qui ne me donne pas le même résultat que la correction.
Je dois trouver les valeurs m et b de l'équation de la droite y(x) m x + bPour se faire j'utilise ces formules:
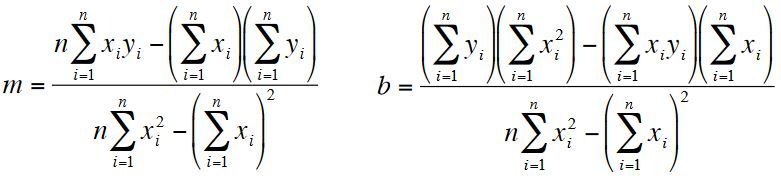
Le tableau a utilisé est:
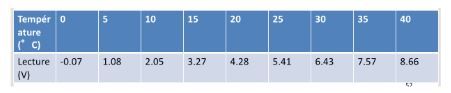
où y est la lecture en volts et x la température.
Mes calculs:
n=9 le nombre de colonnes
m = (9 * 1100.05 - (180 * 38.68)) / 9 * 180² - 180² =0.01133
La correction indique que je devrais trouver y = 0.2176x - 0.0549
Je vous remercie pour votre aide.
-
@dut Bonsoir,
L'erreur est dans le calcul de ∑i=1nxi2\displaystyle\sum_{i=1}^{n}x_i^2i=1∑nxi2,
c'est 02+52+102+.....+4020^2+5^2+10^2+ .....+ 40^202+52+102+.....+402 et non 1802180^21802
-
Ddut dernière édition par
Bonsoir Noemi,
Merci, effectivement je n'avais pas fait attention.
Je refais le calcul demain.Bonne soirée
-
Ddut dernière édition par
Bonjour,
je trouve bien la bonne équation de droite.J'aurais aussi besoin d'un peu aide sur la question suivante:
Calculer la valeur du mesurande et son intervalle de confiance à 95% pour une lecture de 5.72v.J'ai tracé la droite et après une lecture graphique j'en déduis que pour une valeur de 5.72V j'ai une température de 27.29°C
J'aurais besoin d'un petit coup de pouce pour le calcul de l'IC.
Merci
-
Tu dois avoir dans le cours, une formule pour calculer l'intervalle de confiance.
-
Ddut dernière édition par
Mon cours mentionne ça:

Mais je ne comprends pas ce que je dois appliquer
-
Tu appliques ces relations.
Calcule xxx, Sx2S_x^2Sx2 puis x±2Sxx±2S_xx±2Sx
-
Ddut dernière édition par
Alors pour obtenir sx j'enlève le carré c'est à dire sx= sy/m?
Le problème c'est que dans ce calcul je n'ai pas la valeur de sy!
-
Tu dois avoir une formule du type : Sy2=∑i=1n(y−y‾)2nS_y^2=\dfrac{\displaystyle\sum_{i=1}^n (y-\overline y)^2}{n}Sy2=ni=1∑n(y−y)2
-
Ddut dernière édition par
Non rien de la sorte.
y barre: c'est bien la moyenne des y?
-
Oui c'est bien la moyenne.
-
Ddut dernière édition par
Merci Noemi, ça devient plus clair.
Donc pour Sx et Sy pour enlever le carré présent dans les équations, j'utilise les racines carrés?
-
Oui tu prends la racine carrée.
-
Ddut dernière édition par
@Noemi a dit dans Calibrage statique - étalonnage :
Tu dois avoir une formule du type : Sy2=∑i=1n(y−y‾)2nS_y^2=\dfrac{\displaystyle\sum_{i=1}^n (y-\overline y)^2}{n}Sy2=ni=1∑n(y−y)2
Mais en fait je ne peux pas faire le calcul....
je ne connais pas la valeur de y
-
As tu une formule pour le calcul de SyS_ySy ?
y est la lecture en volt.
-
Ddut dernière édition par
non je n'ai que Sx
-
Quelle formule pour SxS_xSx ?
-
Ddut dernière édition par
@dut a dit dans Calibrage statique - étalonnage :
Mon cours mentionne ça:

Mais je ne comprends pas ce que je dois appliquer
-
Ddut dernière édition par
Mais bien sûr si sx^2 la formule ci dessus.
Donc sy^2=sx^2*m
Une fois que j'ai mon résultat j'ajoute une racine carrée pour me débarrasser du carré et j'obtiens la valeur de sy
-
mtschoon dernière édition par mtschoon

Bonjour Dut,
Je n'ai pas suivi ce topic, mais je ne comprends pas ton problème de calcul relatif aux variances et écarts-type.
Je regarde un peu ( mais Noemi est plus à même de te donner des indications vu qu'elle te répond depuis le début)
Tu as indiqué :
J'ai tracé la droite et après une lecture graphique j'en déduis que pour une valeur de 5.72V j'ai une température de 27.29°C
Dans la mesure où tu as trouvé l'équation de la droite : y=0.2176x−0.0549y=0.2176x-0.0549y=0.2176x−0.0549, c'est plus précis de remplacer y par 5.72 et de calculer x (cela évite les erreurs de lecture)
5.72=0.2176x−0.05495.72=0.2176x-0.05495.72=0.2176x−0.0549
0.2176x=5.72+0.05490.2176x=5.72+0.05490.2176x=5.72+0.0549
x=5.72+0.05490.2176x=\dfrac{5.72+0.0549}{0.2176}x=0.21765.72+0.0549
Tu fais le calcul à la calculette . La mienne me donne environ 26,539026,539026,5390
(Tu as même joint la formule directe dans ton dernier message et dans un message précédent).Si ça peut t'arranger, je te donne les calculs à faire pour moyennes, variances, écarts-type de x et de y.
Par contre je ne te donne aucune indication sur" la marge d'erreur sur cette valeur " ni " la formule sur l'intervalle de confiance" car je reste perplexe sur les indications fournies...Moyennes :
x‾=x1+...+xnn\overline{x}=\dfrac{x_1+...+x_n}{n}x=nx1+...+xn avec n=9x‾=0+...+409=20\overline{x}=\dfrac{0+...+40}{9}=20x=90+...+40=20
y‾=y1+...+ynn\overline{y}=\dfrac{y_1+...+y_n}{n}y=ny1+...+yn avec n=9
y‾=−0.07+...+8.669≈4.2977\overline{y}=\dfrac{-0.07+...+8.66}{9}\approx 4.2977y=9−0.07+...+8.66≈4.2977
( vérifie les valeurs car j'ai fait les calculs à la calculette, mais j'ai pu faire une faute de frappe)Variances que j'appelle V(x)V(x)V(x) et V(y)V(y)V(y)
V(x)=∑i=1n(xi−x‾)2nV(x)=\dfrac{ \displaystyle \sum _{i=1}^n (x_i-\overline{x})^2}{n}V(x)=ni=1∑n(xi−x)2
V(x)=(0−20)2+(5−20)2+...+(40−20)29V(x)=\dfrac{(0-20)^2+(5-20)^2+...+(40-20)^2}{9}V(x)=9(0−20)2+(5−20)2+...+(40−20)2
V(y)=∑i=1n(yi−y‾)2nV(y)=\dfrac{ \displaystyle \sum _{i=1}^n (y_i-\overline y)^2}{n}V(y)=ni=1∑n(yi−y)2
V(y)=(−0.07−4.2977)2+...+(8.66−4.2977)29V(y)=\dfrac{(-0.07-4.2977)^2+...+(8.66-4.2977)^2}{9}V(y)=9(−0.07−4.2977)2+...+(8.66−4.2977)2
V(y)V(y)V(y) est calculée avec les valeurs yiy_iyi du tableau.Tu donnes la relation entre V(x)V(x)V(x) et V(y)V(y)V(y) : V(y)=m2V(x)V(y)=m^2V(x)V(y)=m2V(x)
Cette formule, pour V(y)V(y)V(y), utilise l'équation de la droite (elle utilise les ordonnées des points d'abscisse xix_ixi de la droite ; elle n'utilise pas les valeurs yiy_iyi mesurées, mais les valeurs calculées avec l'équation de la droite ).Les deux valeurs ainsi trouvées pour V(y)V(y)V(y) sont seulement légèrement différentes, vu que les points sont "proches" de la droite (le coefficient de corrélation linéaire est très proche de 1)
Ecarts -type ( racines carrées des variances )
Je les appelle σ(x)\sigma(x)σ(x) et σ(y)\sigma(y)σ(y)σ(x)=V(x)\sigma(x)=\sqrt{V(x)}σ(x)=V(x)
σ(y)=V(y)\sigma(y)=\sqrt{V(y)}σ(y)=V(y)Bons calculs.
-
La première étape est d'analyser la différence entre la tension mesurée est la tension théorique obtenue à partir de l'équation de la droite, donc rajouter une ligne au tableau.
Tu calcules ensuite la variance et l'écart type .
Pour un intervalle de confiance à 95% (sauf erreur de calcul), tu obtiens y=5,72±0,08y= 5,72 ±0,08y=5,72±0,08
Tu calcules ensuite la valeur du mesurande xxx, soit x=26,54x=26,54x=26,54
Puis son intervalle de confiance à 95% : 26,17≤x≤26,9126,17 \leq x \leq 26,9126,17≤x≤26,91