Intégrale et fonction en escalier

Bonsoir, j'aurais besoin d'aide svp..
Soit $f$ : $[a; b]$ ---> $R\mathbb{R}$ une application continue telle que $∫ab\displaystyle\int_{a}^{b}$ $f (t) g (t) d t$ =0 pour toutes fonctions en escalier $g$ définie sur $[a; b]$ .
Expliciter $f$ .

@Wil-Fried , bonjour;

A première vue, je dirais que le seule fonction f continue sur [a, b] qui convient est la fonction nulle :
$∀x∈[a,b],f(x)=0\forall x \in [a,b], f(x)=0$

Essaie une démonstration par l'absurde par exemple, ou par contraposée.

@Wil-Fried Bonjour,

Une piste :

Utiliser : $∫abf(t)g(t)dt=[F(t)g(t)]−∫abf(t)g′(t)dt\displaystyle\int_{a}^{b}f(t)g(t)dt = [F(t)g(t)]-\displaystyle\int_{a}^{b}f(t)g'(t)dt$

Bonjour,

@Wil-Fried , je te propose un raisonnement par contraposition pour prouver que f est nécessairement la fonction nulle

Soit $I=∫abf(t)g(t)dt\boxed{I=\int _a^b f(t)g(t) dt}$

Idée :
Par hypothèse, f est continue sur [a,b],
On suppose f non identiquement nulle sur $[a; b]$
On cherche (et on trouve) une fonction g en escalier telle que I est non nulle.
On tire la conclusion.

Une piste possible,

Soit $t_0$ une valeur de $[a, b]$ telle que $f(t0)>0\boxed{f(t_0) \gt 0}$

Vu que f est continue, il existe un intervalle $]t0−α,t0+α[]t_0-\alpha, t_0+\alpha[$ , (avec $α>0\alpha \gt 0$ ), tel que $f(t)>ϵ>0f(t)\gt \epsilon\gt 0$

Choisissons la fonction g en escalier telle que :
$g (t) = 1$ sur $]t0−α,t0+α[]t_0-\alpha, t_0+\alpha[$ et $g (t) = 0$ ailleurs.

$dt\displaystyle I=\int_{t_0-\alpha}^{t_0+\alpha} f(t)\times 1 \ dt$

$dt\displaystyle I=\int_{t_0-\alpha}^{t_0+\alpha} f(t) \ dt$

Vu la propriété de croissance de l'intégrale, vu que $\gt \epsilon$ :
$dt\displaystyle I\gt \int_{t_0-\alpha}^{t_0+\alpha} \epsilon \ dt$

Calculons $dt\displaystyle\int_{t_0-\alpha}^{t_0+\alpha} \epsilon \ dt$ :

$t]t0−αt0+α=ϵ((t0+α)−(t0−α))=2ϵα\displaystyle \int_{t_0-\alpha}^{t_0+\alpha} \epsilon \ dt=\biggr [\epsilon\ t\biggr]_{t_0-\alpha}^{t_0+\alpha}=\epsilon((t_0+\alpha)-(t_0-\alpha))=2\epsilon\alpha$

or $2ϵα>02\epsilon\alpha \gt 0$

Donc $I>0I\gt 0$ donc $I≠0I\ne 0$

Bonne réflexion.
Si ce raisonnement te convient, tu pourras faire le même type raisonnement avec $f(t0)<0f(t_0) \lt 0$

@Wil-Fried , si tu veux "creuser" les types de raisonnement, je te mets un lien :
http://www.toupie.org/Dictionnaire/Contraposition.htm

Pour démontrer que $A$ => $B$ , on peut démontrer la proposition contraposée $n o n B$ => $n o n A$

Dans l'explication que je t'ai indiquée , f étant continue , on a :

$A$ : pour toute fonction g en escalier , $I = 0$
$B$ : f fonction nulle
On veut prouver que $A$ => $B$

$n o n B$ : f fonction non nulle
$n o n A$ : il existe une fonction g en escalier telle que $I≠0I\ne 0$

Ainsi, en prouvant $n o n B$ => $n o n A$ , on prouve que $A$ => $B$ , vu que ce sont des propositions équivalentes.

Bonne réflexion.

Re-bonjour,

@Noemi a dit dans Intégrale et fonction en escalier :

@Wil-Fried Bonjour,

Une piste :

Utiliser : $∫abf(t)g(t)dt=[F(t)g(t)]−∫abf(t)g′(t)dt\displaystyle\int_{a}^{b}f(t)g(t)dt = [F(t)g(t)]-\displaystyle\int_{a}^{b}f(t)g'(t)dt$

Utiliser g'(t) sur [a,b] me laisse perplexe pour une démonstration générale directe.
L'énoncé indique que l'intégrale est nulle pour toute fonction en escalier définie sur [a,b].
Mais, toute fonction en escalier définie sur [a,b] n'est pas dérivable sur [a,b].

Cela convient seulement dans le cas où g est constante sur [a,b] ; dans ce cas, g est dérivable sur [a,b]; g'(t) existe et vaut 0.
Mais, lorsque g prend au moins deux valeurs distinctes sur [a,b], g n'est pas dérivable en au moins un point, donc g'(t) n'est pas définie en au moins un point. g'(t) n'est pas définie sur [a,b].

Un exemple pour illustrer.

Soit g , en escalier, définie sur $[a, b]$ par :
$g (t) = 1$ sur $[a,a+b2[\biggr [a, \dfrac{a+b}{2}\biggr[$ et $g (t) = 2$ sur $[a+b2,b]\biggr[\dfrac{a+b}{2},b\biggr]$

g n'est pas dérivable en $t=a+b2t=\dfrac{a+b}{2}$

Démonstration :

$lim⁡h→0+g(a+b2+h)−g(a+b2)h=lim⁡h→0+2−2h=0\displaystyle \lim_{h \to 0^+}\dfrac{g(\dfrac{a+b}{2}+h)-g(\dfrac{a+b}{2})}{h}=\lim_{h \to 0^+}\dfrac{2-2}{h}=0$
g dérivable à droite en $t=a+b2t=\dfrac{a+b}{2}$ et le nombre dérivé à droite vaut 0

$lim⁡h→0−g(a+b2+h)−g(a+b2)h=lim⁡h→0−1−2h=+∞\displaystyle \lim_{h \to 0^-}\dfrac{g(\dfrac{a+b}{2}+h)-g(\dfrac{a+b}{2})}{h}=\lim_{h \to 0^-}\dfrac{1-2}{h}=+\infty$
g non dérivable à gauche en $t=a+b2t=\dfrac{a+b}{2}$

d'où la conclusion.

Dans ce cas, on ne peut pas utiliser g'(t) sur [a,b]

@Wil-Fried , bonjour,
Cet exercice n'est pas aussi simple qu'il parait être à première vue...
Je vois que tu es passé plusieurs fois sur le forum.
Peut-être as-tu consulté les pistes données.
Si c'est le cas et si tu as un souci sur une démonstration, ne te gène pas, demande.

Bon travail !

@mtschoon Bonjour, effectivement j'ai essayé de comprendre ce que vous avez donné comme piste.. mais franchement je comprend pas grandes choses.

@Wil-Fried , bonjour,

Je m'en doutais un peu...

La démarche est une démarche de "Supérieur", c'est sûr...

Pourrais-tu préciser où tu bloques .

ou bien sur l'utilisation du fait que f est continue en $t_0$ avec $f(t0)>0f(t_0)\gt 0$ ?
ou bien sur la fonction g choisie ?
ou bien sur le principe de contraposition ?

@mtschoon Effectivement, sur tout votre raisonnement par contraposition. Incluant f et g.

@Wil-Fried , j'essaie d'expliciter.

i) Contraposition.

Regarde ce que je t’ai indiqué précédemment sur cette notion et le lien fourni.

Si tu as un cours de Sup sur la logique, ces notions de contraposée, quantificateurs universels, existentiels, doivent t’être familières. Si ce n’est pas le cas, tu découvres...

En logique, la contraposée d'une proposition « A implique B » est l’implication : « non B implique non A »
Ces propositions sont équivalentes : (A => B) <=> (non B => non A)

Lorsque la démonstration directe de A=> B est « délicate » voire pas possible, on peut, à la place, si c’est plus simple, démontrer que non B => non A

Pour l’étude proposée :
Soit f continue de [a,b] vers $R$
La contraposée de " pour toute fonction g en escalier telle que $f(t)g(t)dt=0\int_a^b\ f(t)g(t)dt=0$ implique f nulle sur [a,b]" est :
"f non nulle sur [a,b] implique il existe une fonction g en escalier telle que $f(t)g(t)dt≠0\int_a^b\ f(t)g(t)dt\ne 0$ "

ii) Pour f continue sur [a,b] et non nulle sur [a,b],

Vu que f est non nulle, j'ai choisi le cas où, pour une valeur $t_0$ , $f(t_0)$ prend une valeur strictement positive. (j'aurais pu aussi bien prendre une valeur strictement négative- le raisonnement aurait été le même).

Pour t'éclairer, j'ai fait un schéma
Représentation de f au voisinage de $t_0$ en bleu
droite $y=ϵy=\epsilon$ en rouge
droites $x=t_0-h$ et $x=t0+αx=t_0+\alpha$ en vert.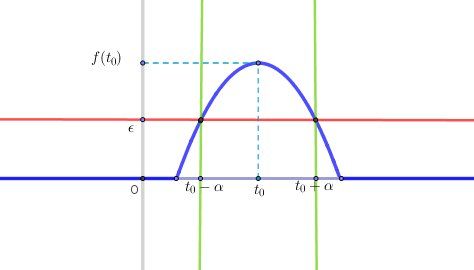

Relis ce que je t'ai indiqué sur cette question précédemment (je ne re-écrit pas tout) en t'aidant du schéma.

iii) Pour la fonction g choisie.

J'ai choisi la fonction g en escalier telle que :
$g (t) = 1$ pour $t∈]t0−α,t0+α[t\in ]t_0-\alpha, t_0+\alpha[$
$g (t) = 0$ pour $t∈Rt\in R$ \ $]t0−α,t0+α[]t_0-\alpha, t_0+\alpha[$

Si tu revois les calculs faits dans mon message précédent correspondant, tu trouveras :
$∫abf(t)g(t)dt=0+∫t0−αt0+αf(t)g(t)dt+0\int_a^b f(t)g(t)dt= 0+\int_{t_0-\alpha}^{t_0+\alpha}f(t)g(t)dt+0$

Après calculs (déjà faits- revois les)
$∫abf(t)g(t)dt>0\int_a^b f(t)g(t)dt\gt 0$
donc
$∫abf(t)g(t)dt≠0\int_a^b f(t)g(t)dt\ne 0$
CQFD.

J'espère que ces éléments t'éclaireront .

Bon courage et Bonne lecture.