système linéaire de matrice
-
MMOUNA8 dernière édition par
bonjour, je voudrais une correction pour l'exercice que j'ai fait :
On étudie l’évolution dans le temps d’une population animale. À la date n (en années),
cette population se divise en xn jeunes et yn adultes. L’année comporte une saison hivernale et une saison de reproduction.
Lors de la saison hivernale, 40% des jeunes survivent et deviennent des adultes et 80% des adultes survivent.
Lors de la saison de reproduction, chaque adulte donne naissance à 2 jeunes (en fait 4 par femelle). Tous les adultes survivent.
a) Exprimez xn+1 et yn+1 en fonction de xn et yn. Ecrivez le système obtenu sous forme matricielle.
b) Calculez xn et yn en fonction de x0 et y0 du début de l’observation.voilà ce que j'ai fait :
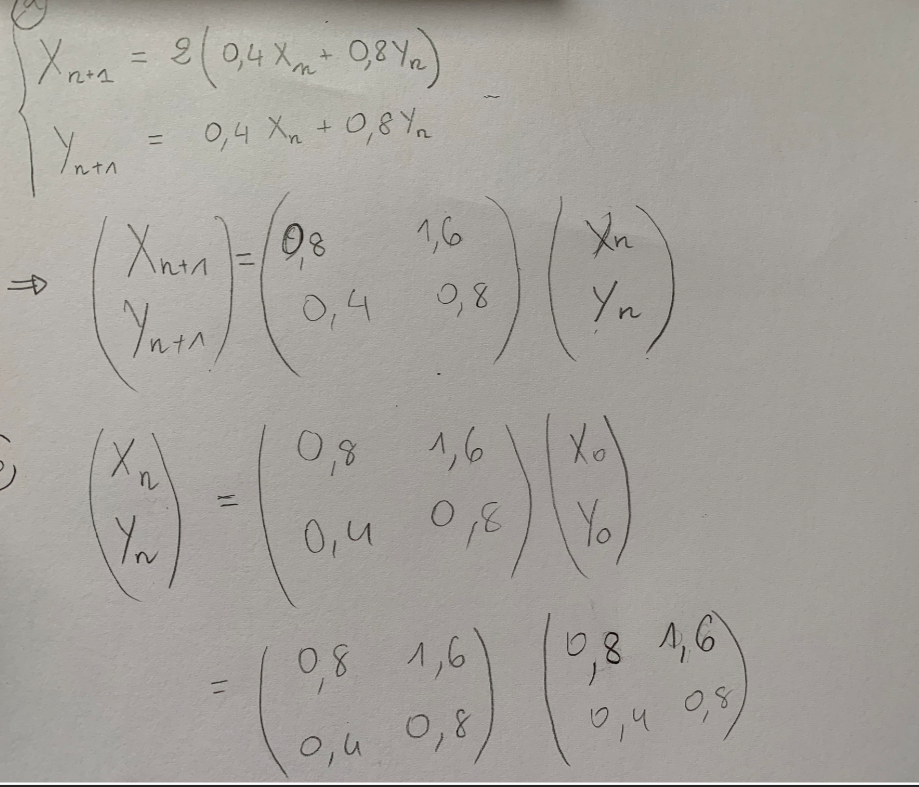
-
mtschoon dernière édition par mtschoon

@mimims , re-bonjour,
OK pour le a)
Je ne comprends pas bien ce que tu as écrit au b)
Soit
A=(0.8 1.60.4 0.8)A=\begin{pmatrix} 0.8\ \ 1.6 \cr 0.4\ \ 0.8 \end{pmatrix}A=(0.8 1.60.4 0.8)(xn+1yn+1)=A(xnyn)\begin{pmatrix} x_{n+1} \cr y_{n+1} \end{pmatrix}=A\begin{pmatrix} x_{n} \cr y_{n} \end{pmatrix}(xn+1yn+1)=A(xnyn)
Tu as une suite géométrique de matrices, de raison A et de premier terme (x0y0)\begin{pmatrix} x_{0} \cr y_{0} \end{pmatrix}(x0y0)
Donc,
(xnyn)=An(x0y0)\begin{pmatrix} x_{n} \cr y_{n} \end{pmatrix}=A^n\begin{pmatrix} x_{0} \cr y_{0} \end{pmatrix}(xnyn)=An(x0y0)
-
mtschoon dernière édition par

Bonjour,
Un complément,
Vu que Connaissance a re-ouvert ce topic, je regarde la fin.
Pour donner xnx_nxn et yny_nyn, séparément, en fonction de x0x_0x0 et y0y_0y0, il faut expliciter AnA^nAn .
Après transformation, on peut trouver, par exemple, :
An=(1.6)n4(2 41 2)A^n=\dfrac{(1.6)^n}{4}\begin{pmatrix}2\ 4\cr1\ 2\end{pmatrix}An=4(1.6)n(2 41 2)d'où, après calcul matriciel :
xn=(1.6)n4(2x0+4y0)x_n=\dfrac{(1.6)^n}{4}(2x_0+4y_0)xn=4(1.6)n(2x0+4y0)yn=(1.6)n4(x0+2y0)y_n=\dfrac{(1.6)^n}{4}(x_0+2y_0)yn=4(1.6)n(x0+2y0)
-
Lleohnye dernière édition par
@mtschoon
Bonsoir Monsieur
N'existe t'il pas autre méthode ?
-
mtschoon dernière édition par

@leohnye , bonsoir,
La réponse proposée correspond aux questions demandées.